前言
上一篇介绍了Double DQN对DQN的目标Q值优化,这篇将介绍在DDQN的基础上,对经验回放池的优化
一、论文题目
PRIORITIZED EXPERIENCE REPLAY
二、研究目标
在DDQN基础上,改进经验回放池的均匀随机采样算法,使得学习更高效
三、问题定义
DDQN的均匀随机采样问题
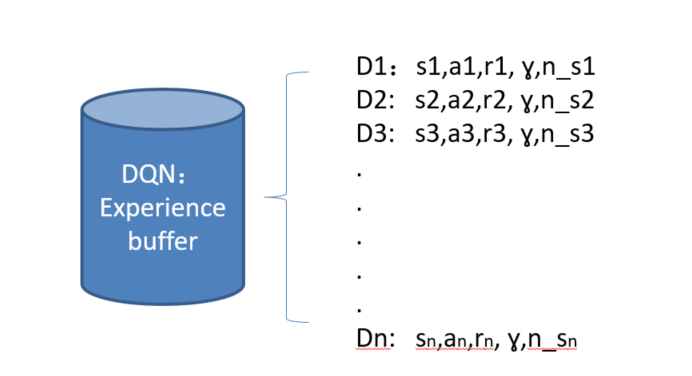
以往的DQN或DDQN的做法是从buffer中均匀随机采样,这样会导致一些有用的样本可能被抽到的次数少,并且存储数据的空间有限,当空间存满之后,每次放入一个experience就要丢弃先前的一个experience。那么就要思考下面两个问题
- 选择那些experience保存
- 选择那些experience被回放
四、PRIORITIZED REPLAY 方法介绍
作者针对上面的两个问题,着重解决的是第二个问题,即选择那些experience被回放
4.1 举例说明
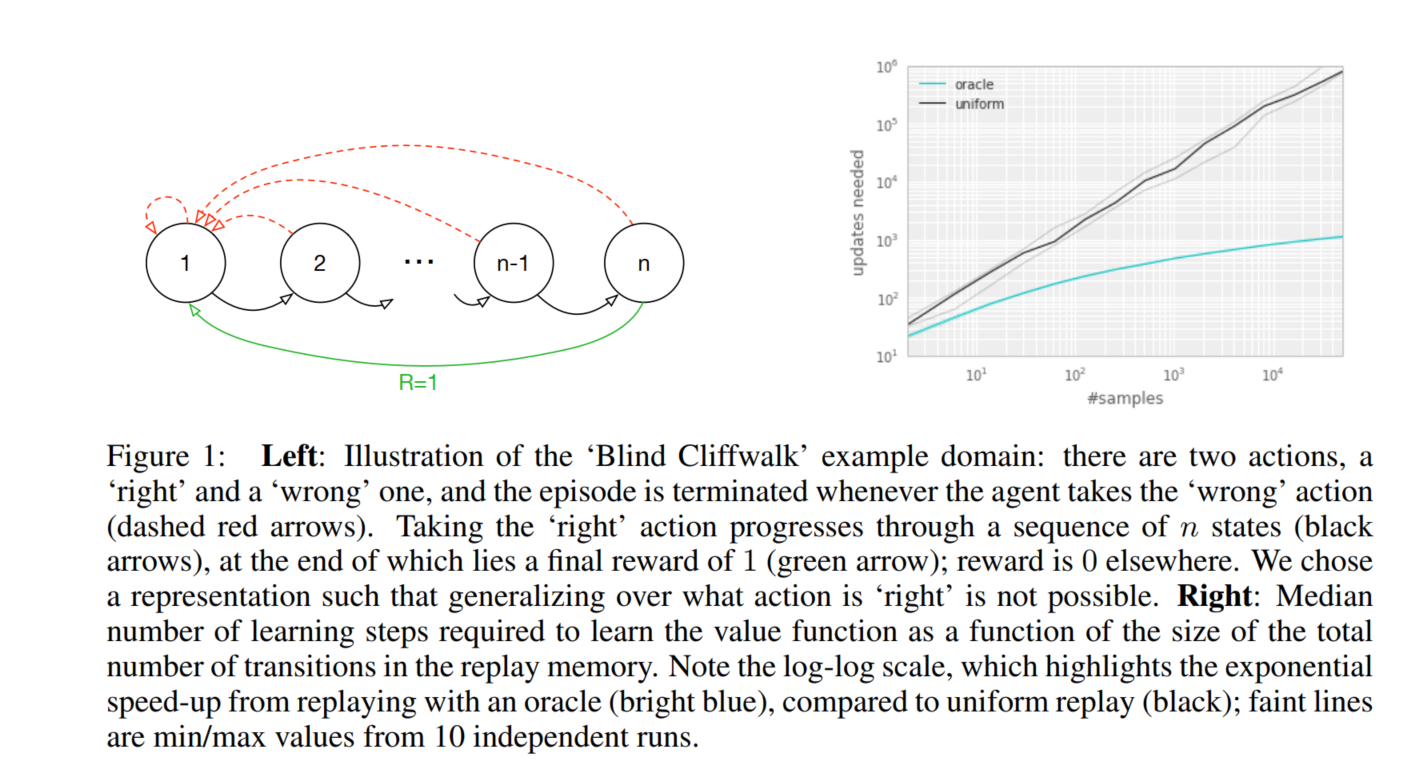
如上图所示,本文给出了一个例子来充分的说明优先的潜在好处。引入了称为“Blind Cliffwalk”的环境,来示例说明当奖赏非常 rare的时候,探索所遇到的挑战。假设仅有 n 个状态,这个环境就要求足够的随机步骤直到得到第一个非零奖励;确切的讲,随机的选择动作序列就会有 2^(-n)的概率才能得到第一个非零奖赏。此外,最相关的 experience却藏在大量的失败的尝试当中。
本文利用这个例子来显示了两个agents的学习次数的不同。可以看到这两个agent都从同一个经验回放池中去获取Q-learning的更新,第一个agent随机均匀采样experience,第二个agent唤醒一个oracle来进行优先级experience采样。这个oracle贪婪的选择使得在当前状态下最大化降低全局损失的experience。
从上图右侧,也能看出,按照一定优化序列得到的experience比均匀随机采样要花费很少的尝试步骤,这明显的提升了训练速度。
注:这里的oracle可以理解为上帝,文中的意思指的是实验跑完了,回过来看如何如何做最好,相当于一种离线学习,即oracle采样的数据是最好的一组batch
4.2 Prioritizing with TD-Error
Temporal-difference(TD)error表示一个experience的惊奇度或出乎意料的程度
引入TD-Error:引入TD-Error的目的是给每一个experience添加一个TD-Error标准,在每次进行更新时,从buffer中选择绝对值对打的TD-Error的样例进行回放。然后对该样例进行Q-learning的更新,更新Q值和TD-Error的权重。新的experience到来之后,没有已知的 TD-error,所以我们将其放到最大优先级的行列,确保所有的 experience 至少回放一次。
TD-Error公式如下:
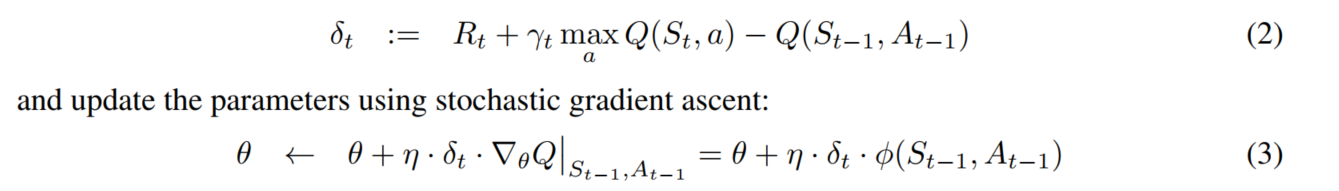
引入TD-Error后的好处:
oracle的做法可以极大的降低无用的尝试,加速了算法的执行速度
4.3 Stochastic Priorization
引入 Stochastic Priorization的目的是为了缓解多样性的损失
在上一步引入TD-Error后会产生两个问题:
为了避免消耗太多资源遍历整个memory,我们只为那些被replay的experience更新TD-error;如果一开始就被赋予一个很低的TD-error,在很长一段时间内可能都不会被replay
贪婪优先集中于一个小的经验子集,误差收缩的很慢,特别是使用函数估计的时候,意味着初始的高误差转移被经常回放。缺乏多样性使得该系统倾向于 over-fitting
(为什么丧失多样性造成过拟合:对于DQN,回放就是把经验池中取出的experience中的s状态输入到Q-network中,next state 输入到target Q-network中,然后进行一系列计算loss,反向传播更新网络参数,如果一直重复这一条信息输入,那么我对于训练网络过程来说精度会很高,而当测试的时候,输入别的状态就会使测试精度降低,即过拟合)
对 noise spikes 非常敏感,bootstrapping 会加剧该现象,估计误差又会成为另一个噪声的来源
为了解决上述问题,我们引入了一个随机采样的方法,该方法结合了 纯粹的贪婪优先 和 均匀随机采样。我们确保被采样的概率在experience优先级上是单调的,与此同时,确保最低优先级的experience的概率也是非零的。具体的,我们定义采样experience i 的概率为:
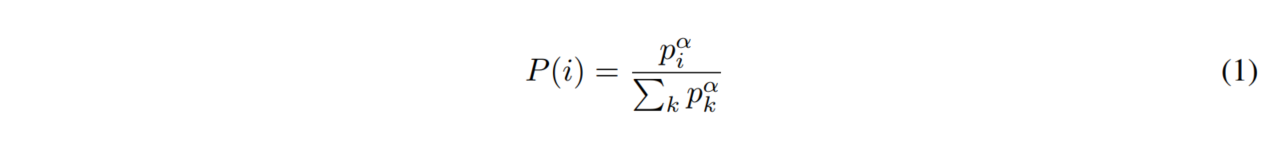
其中,pi 是experience i 的优先级。指数 α 决定了使用多少优先级,当 α 等于 0 的时候是均匀的情况
pi有以下两种变体:
直接的、成比例优先(Proportional Variant):
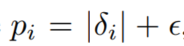
这里的
是一个很小的数字,这样就保证了有些TD-Error为0的特殊边缘例子也能够被采样到
间接的、基于排行的优先(Rank-based Variant):
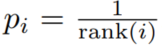
rank(i)是根据
排序后,i 的排名
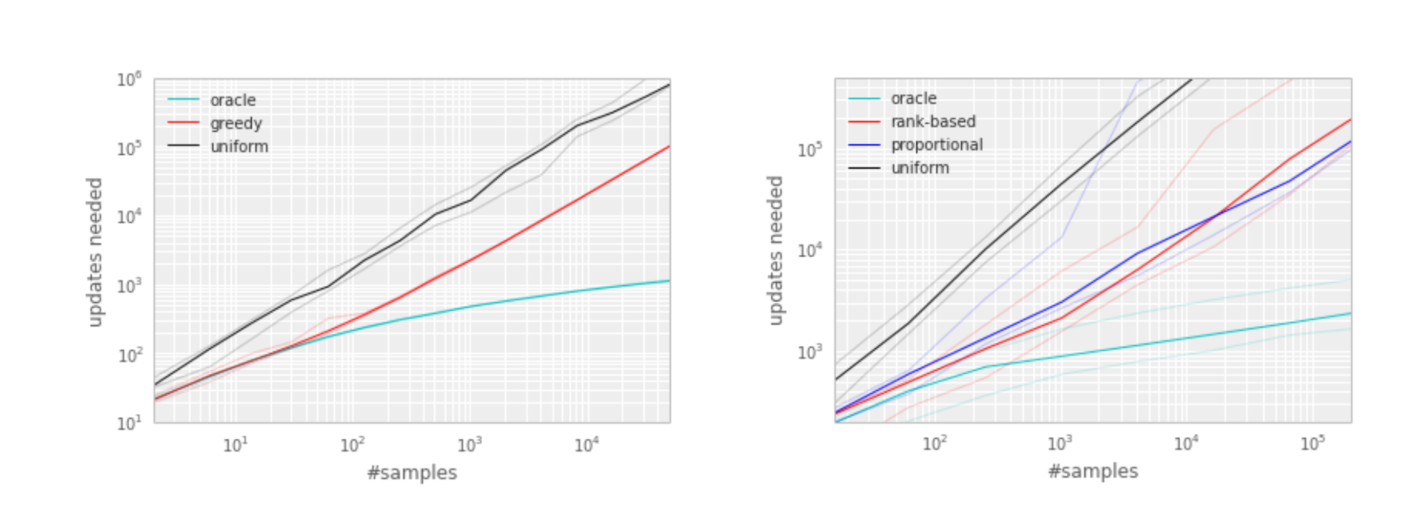
两个分布都是随着误差单调的,但是后者更鲁棒,因为其对离群点不敏感。两个变体相对均匀的baseline来讲都是有很大优势
4.3.1 Proportional Variant
本文提出的Sum Tree,Sum Tree是一种树形结构,每片树叶存储每个样本的优先级
p, 每个树枝节点只有两个分叉, 节点的值是两个分叉的合, 所以 SumTree 的顶端就是所有p的合. 正如下面图片(来自Jaromír Janisch), 最下面一层树叶存储样本的p, 叶子上一层最左边的 13 = 3 + 10, 按这个规律相加, 顶层的 root 就是全部p的合了.
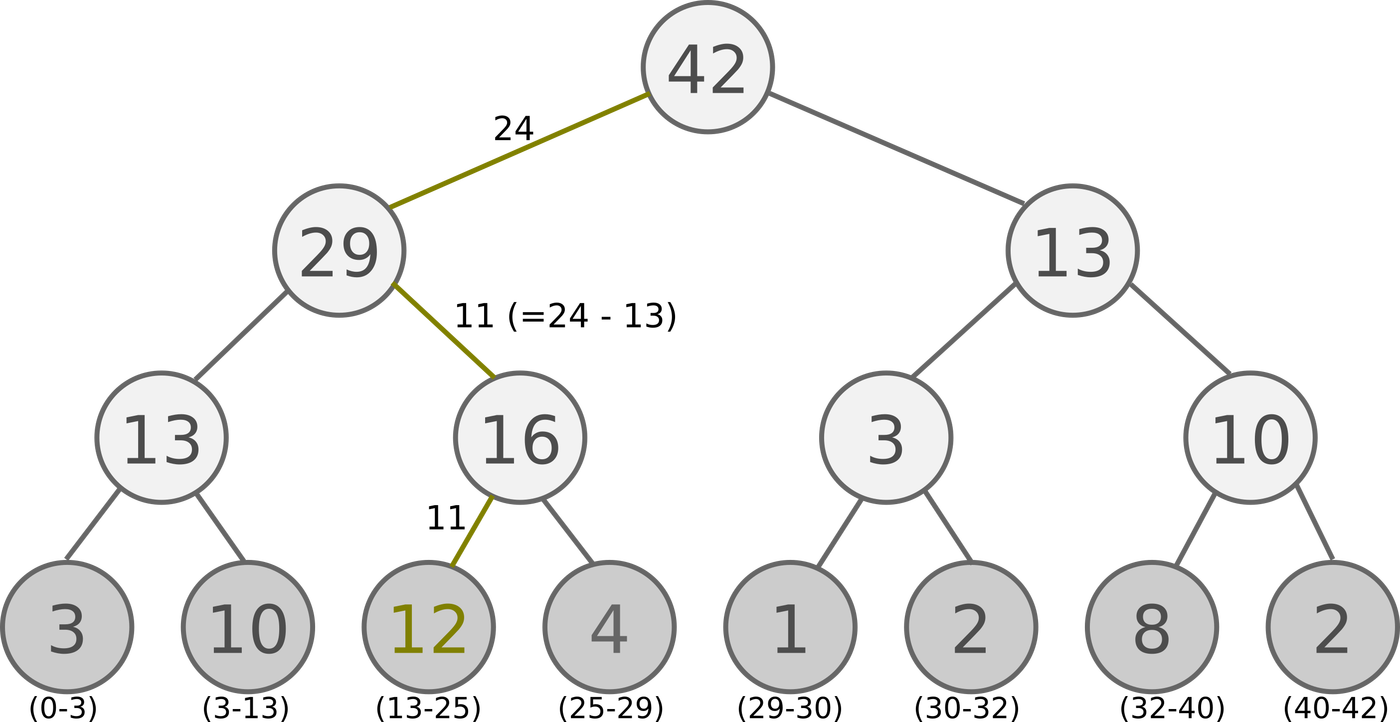
抽样时, 我们会将 p 的总合 除以 batch size, 分成 batch size 那么多区间, (n=sum(p)/batch_size). 如果将所有 node 的 priority 加起来是42的话, 我们如果抽6个样本, 这时的区间拥有的 priority 可能是这样.
[0-7], [7-14], [14-21], [21-28], [28-35], [35-42]
然后在每个区间里随机选取一个数. 比如在第区间 [21-28] 里选到了24, 就按照这个 24 从最顶上的42开始向下搜索. 首先看到最顶上 42 下面有两个 child nodes, 拿着手中的24对比左边的 child 29, 如果 左边的 child 比自己手中的值大, 那我们就走左边这条路, 接着再对比 29 下面的左边那个点 13, 这时, 手中的 24 比 13 大, 那我们就走右边的路, 并且将手中的值根据 13 修改一下, 变成 24-13 = 11. 接着拿着 11 和 13左下角的 12 比, 结果 12 比 11 大, 那我们就选 12 当做这次选到的 priority, 并且也选择 12 对应的数据.
注:上面的说明是参照的网上教程写的,这里在写一下自己的理解
个人理解:图片中的所有叶子节点(3、10、12、4、1、2、8、2)对应于每一个experience的TD-Error,然后两个两个组合,构成哈夫曼树,即会生成顶层的根root,并且其值为42。然后在进行分区,分区后再每个区间进行抽值,如抽到的为n。抽值后,从根节点开始找(从上至下,从左至右),如果遇见其子节点m比n大,则走该子节点的路,如果遇见子节点m比n小,则走另一个子节点路,并且n=n-m.,直到找到叶子节点,选择叶子节点中那个比当前n值大的experience。
4.3.2 Rank-based Variant
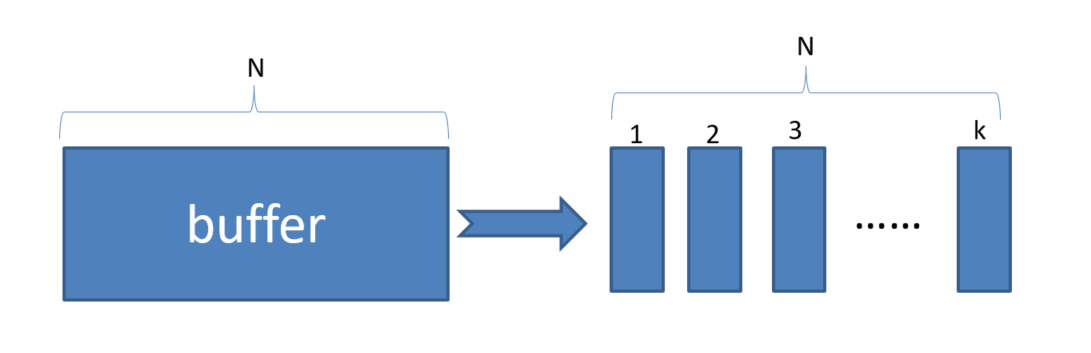
将buffer分为k个等概率的分段,从每一个分段中进行贪婪优先采样
4.4 Annealing the bias
利用随机更新得来的期望值的预测依赖于这些更新,对应其期望的同样的分布。优先回放引入了误差,因为它以一种不受控的形式改变了分布,从而改变了预测会收敛到的 solution(即使 policy 和 状态分布都固定)。我们可以用下面的重要性采样权重(importance-sample weights)来修正该误差:
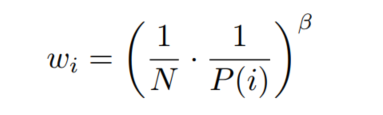
Importance sampling的影响:
在典型的强化学习场景中,更新的无偏性在训练结束接近收敛时是最重要的,因为由于策略、状态分布和引导目标的改变,有bias会高度不稳定,与未修正的优先重放相比,Importance sampling使学习变得不那么具有侵略性,一方面导致了较慢的初始学习,另一方面又降低了过早收敛的风险,有时甚至是更好的最终结果。与uniform重放相比,修正的优先级排序平均表现更好。
4.4 本文采用方法
本文将优先回放和 Double Q-learning 相结合,就是将 均匀随机采样 替换为 本文提出的 随机优先和重要性采样方法,具体算法见下图

总结
Prioritized Replay DQN和DDQN相比,收敛速度有了很大的提高,避免了一些没有价值的迭代,因此是一个不错的优化点。同时它也可以直接集成DDQN算法,所以是一个比较常用的DQN算法。