前言
DDQN对DQN的目标Q值进行优化,去除max操作来减少过度估计的问题,Prioritized Replay DQN对DQN的经验回访池进行优化,给每个experience一个权重值,并按权重采样来优化算法提高训练速度,而这篇博客即将介绍的是Dueling DQN,对DQN的神经网络结构进行优化
一、论文题目
Dueling Network Architectures for Deep Reinforcement Learning
二、研究目标
改进DQN的神经网络结构来加快学习速率
三、问题定义
DQN的神经网络结构优化问题
- 以往的DQN网络最后的输出为每个action的Q-values值(在某个确定的状态下)。但是对于许多状态,根本没有必要去预测每个action对应的Q-value值
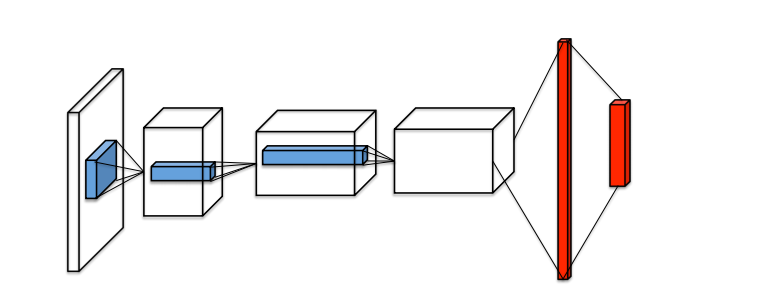
四、Dueling DQN方法介绍
Dueling DQN将Q网络分成两部分:
第一部分仅仅与状态S有关,与具体要采用的动作A无关,这部分称为状态价值函数部分,记
第二部分同时与状态S和动作A有关,这部分称为动作优势函数,记
其中,theta是卷积层参数,alpha和beta分别是两只路的全连接层参数
4.1 Dueling DQN网络结构
Dueling DQN的网络结构如下图第二个网络结构
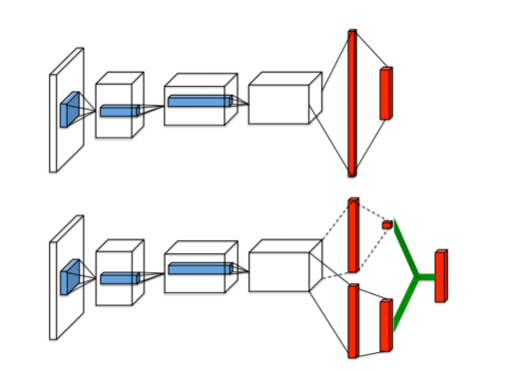
如上图所示,第一个网络结构是一般的DQN网络模型(输入层->三个卷积层->两个全连接层->输出每个动作的Q值)
而第二个网络结构则是本文即将介绍的Dueling DQN网络模型,Dueling DQN将卷积层提取的抽象特征分流到两个支路中。其中上路代表的是状态价值函数V(s),表示静态的状态环境下本身具有的价值,它表明了状态的好坏程度;下路代表的是依赖状态的动作优势函数A(s,a),表示在某个状态下,选择某个action额外带来的价值,它表明了在这个状态下各个动作的相对好坏程度。最后这两路聚合在一起得到每个动作的Q值。
最终Dueling DQN可以如下图:
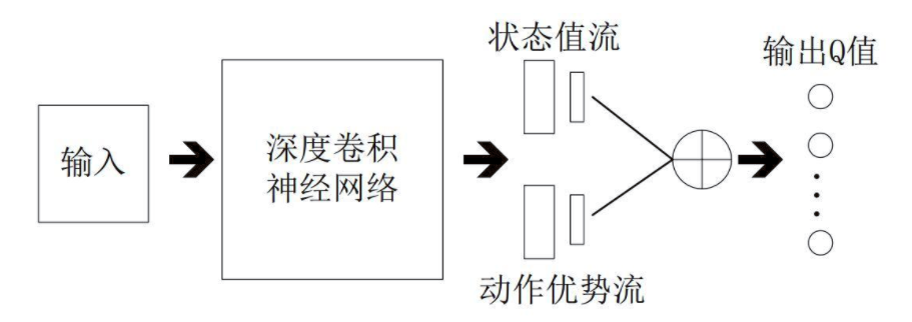
注:
V(s):V(s)表示状态本身的好坏,一般为一个值(标量)
A(s,a):A(s,a)表示当前状态下采取的行动的好坏,一般为n个值,因此A(s,a)决定了策略
4.2 Dueling DQN的Q值
由前面可知,Q值由V(s) 和A(s,a)合并得到,其Q值的公式如下
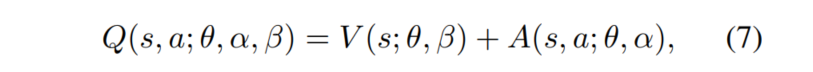
其中,theta是卷积层参数,beta是V(s)的全连接层参数,alpha是A(s,a)的全连接参数
但是上面的公式也存在一些问题,效果并不好,因为它不具备可辨识性:通过Q值无法反过来确定V和A。
因此,可以强制令所选择的贪婪动作优势函数为0:
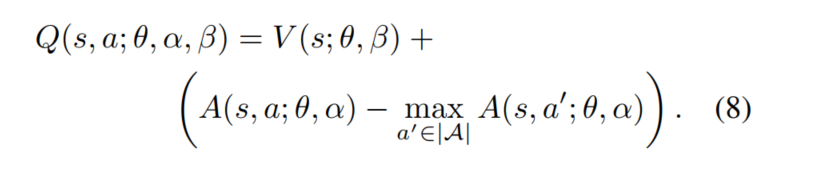
这样我们就能得到唯一的值函数:
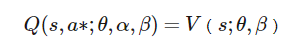
其中,a*如下:
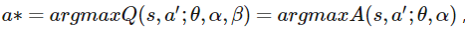
说明:在公式(8)中减去了一个最优的a所对应A值,这样A-A就为0了,A本身就是要寻找到最合适的a,然后确定A值,这样Q值就等于V值,并且V网络给出了最优V-值的估计,那么相应的A网络也给出了A的估计
但是在实际操作中,我们采用的方法是减去A的平均,本文的Dueling DQN方法就是采用的这种方式,因此,公式(8)修改为公式(9):
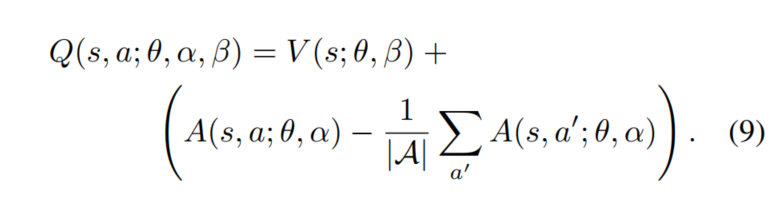
虽然这样得到的V和A不在是具有真实意义的V和A,但是能增加稳定性(因为采用 -max会在更新时损害最优A的值),并且通过减去A的平均能有以下三个优点:
- 平均值和最大值的测试结果非常类似,但是平均值公式比较简洁
- 没有改变A(s,a)的相对顺序,保证了该状态下各个动作的优势函数相对顺序不变,保留了Dueling DQN的Q值的所有性质
- 能够去除多余的自由度,提高算法的稳定性
4.3 举例说明
Dueling DQN能学习到在没有动作的影响下环境状态的价值V(s)。如下图
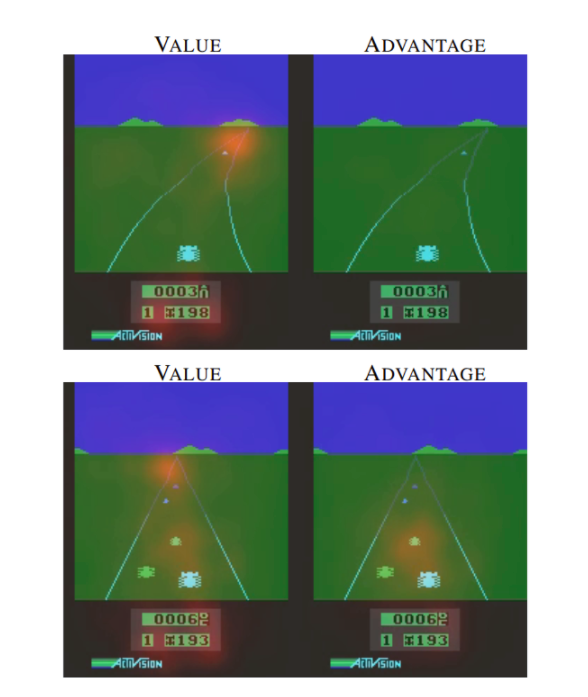
下图中的左右两列分别表示V(s)和A(s,a),图中的红色区域表示V(s)和A(s,a)所关注的地方
在训练过程中,V(s)关注地平线上是否有车辆出现(此时动作的选择影响不大)以及分数,如下图第一行;而A(s,a)则更关心会立即造成碰撞的车辆,此时动作的选择很重要,如下图第二行
五、实验
5.2 实验方法
采用方法:Dueling DQN + DDQN + Prioritized Replay DQN
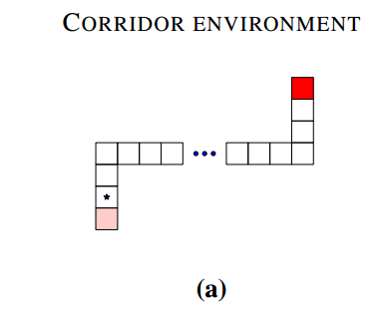
MDP:
- 状态集:70(水平50,两垂直各10)
- 行为集:5(上、下、左、右、无操作)
- 转换函数:model free
- 奖励函数:红点获得正面奖励
- 起始状态:左下角
- 结束状态:右下角
5.2 实验结果
当行为越多时,dueling DQN的性能就更好
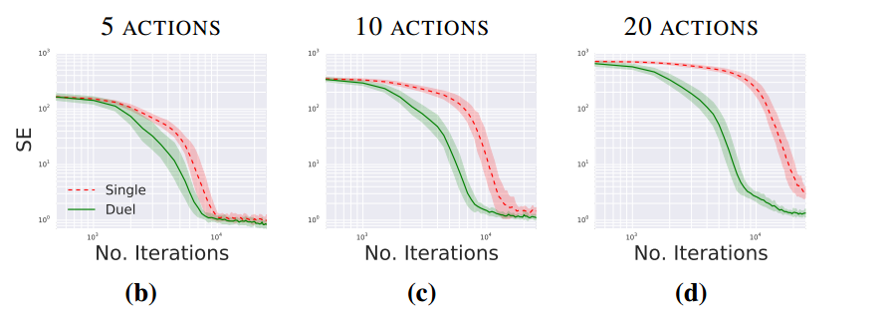
其中,5,10,20的含义是:5个行为时表示上下左右、无操作共五个,而10和20则分别是在5个行为的基础之上添加了5个和15个无操作行为。SE表示平方误差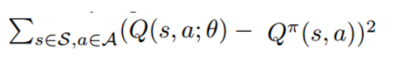
六、结论
Dueling DQN的优势部分在于其有效学习状态值函数的能力
- V函数可以得到更多的学习机会,因为以往一次只更新一个动作对应的Q值
- V函数的泛化性更好,当动作越多时,优势越明显。直观上看,当有新动作加入时,它并不需要从零开始学习
- 因为Q函数在动作和状态的维度上的绝对值往往差很多,这会引起噪声和贪婪策略的突变,使用Dueling DQN可以改善这个问题
总结
到目前为止,关于DQN的方法和有关DQN的优化方面,算是已经全部阅读完了,后续要在开始看其他的DRL论文,后面要加强的是这几种方法的一些小训练测试