DRL论文阅读（五）之Policy Gradient理解

前言

在前面的四篇DQN强化学习算法中，主要是对价值函数进行了近似表示，这是只一种基于价值函数（Value Based）的方法，是基于状态价值函数V(s)或者动作价值函数Q(s,a)的控制问题解法。在确定性的环境中，当我们知道了每个状态价值函数V(s)的数值之后，策略就可以选择使得下一个状态期望状态价值函数最大的行动a。但是在随机的环境中状态价值函数V(s)就不太好用了，因为它不能直接指导我们进行行动的选择。因此，在控制问题中更常用的是动作价值函数Q(s,a)，它描述了在某个状态s下采取不同的行动a产生的期望收益。但是这是一种间接的做法，那有没有更直接的做法呢？

有！那就是直接更新策略。本文将介绍一种更为直接的方式解决强化学习中的控制问题—策略梯度方法，它属于另一类，即基于策略的方法（Policy Based）。

一、论文题目

Policy Gradient Methods for Reinforcement Learning with Function Approximation

二、研究目标

研究一种更直接的方法解决强化学习中的控制问题，之前的控制方法是一种间接方法

三、问题定义

3.1 Value Based方法的局限性

首先，它面向的是确定性策略，而最优策略通常是随机的
其次，DQN系列方法对连续动作的处理能力不足。如果在一个连续空间内挑选动作，则Q值将会在无穷多的动作中计算价值，从而选择行为，这可吃不消
最后，算法收敛障碍。一个行动的估计值的任意小的变化可以导致它被选择或不被选择，这种不连续变化是算法保证收敛的一个关键障碍

3.2 Policy Based方法的优缺点

优点：

连续的动作空间（高维空间）中更加高效
可以实现随机化的策略
某种情况下，价值函数可能比较难以计算，而策略函数比较容易

缺点：

通常收敛到局部最优而非全局最后
评估一个策略通常低效（这个过程可能慢，但是具有更高的可变性，其中也会出现很多并不有效的尝试，且方差高）

四、Policy Gradient算法介绍

4.1 Value Based网络

在Value Based强化学习方法中，我们对价值函数进行了近似表示，引入了一个动作价值函数Q，这个函数由参数w描述，并接受状态s与动作a的输入，计算后得到近似的动作价值，即：

$Q(s,a,w)\equiv\pi(s,a)$

4.2 Policy Network

Policy Gradient 基本思想就是通过更新Policy Network来直接更新策略

Policy Network：实际上就是一个神经网络，输入是状态，输出直接就是动作（不是Q值）

输出一般有以下两种方式：

概率方式：输出某一个动作的概率
确定性方式：输出具体的某一个动作

举例如下图所示：输入当前的状态，输出action的概率分布，选择概率最大的一个action作为要执行的操作。

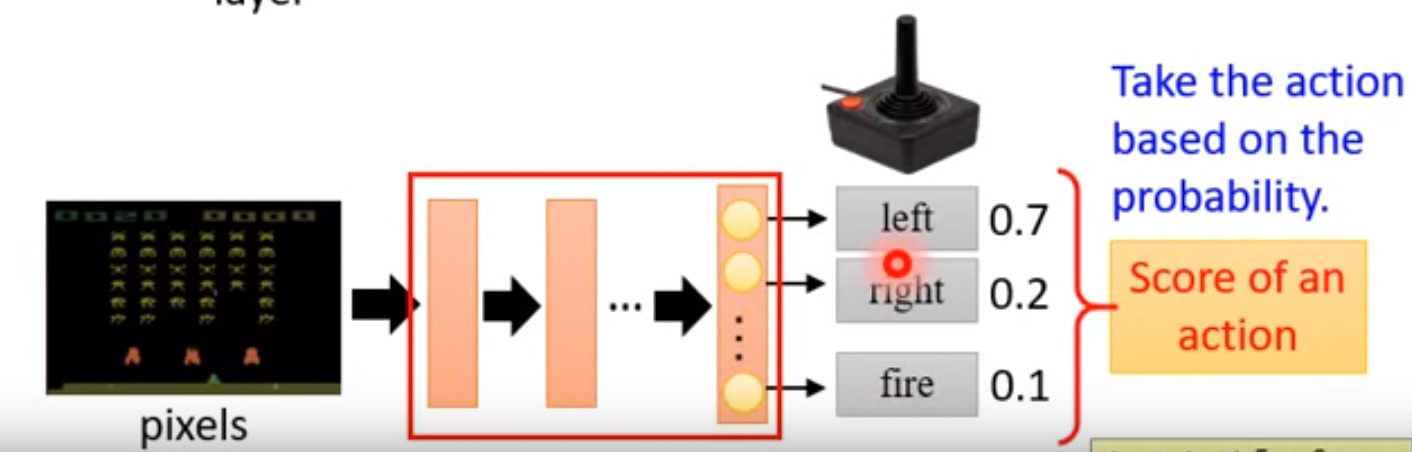
在Policy Based强化学习方法下，我们采样类似的思路，只不过这时我们对策略进行近似表示。此时策略π可以被描述为一个包含参数θ的函数,即：

$\pi_\theta(s,a) = P(a|s,\theta) \equiv\pi(a|s)$

Policy Based的方法就是使用参数θ来逼近拟合状态值函数Vπ（s）和状态动作值函数Qπ（s，a）的分布。

$V_\theta(s) \equiv V_\pi(s)$ $Q_\theta(s,a) \equiv Q_\pi(s,a)$

将策略表示成一个连续的函数后，我们就可以用连续函数的优化方法来寻找最优的策略了。而最常用的方法就是梯度上升法了，那么这个梯度对应的优化目标如何定义呢？

4.3 更新Policy Network

Policy Gradient不通过误差反向传播，它通过观测信息选出一个行为直接进行反向传播，当然出人意料的是他并没有误差，而是利用reward奖励直接对选择行为的可能性进行增强和减弱，好的行为会被增加下一次被选中的概率，不好的行为会被减弱下次被选中的概率。

如果要更新 Policy Network 策略网络，或者说要使用梯度上升的方法来更新网络，需要有一个目标函数，且此时的策略Policy参数化为

$\pi_\theta(s,a) = P(a|s,\theta) \equiv\pi(a|s)$

使用model-free的方法，不借助与agent做决策而是将agent丢入不确定的动态环境下，不提供动态环境的信息，让agent自己瞎溜达根据所获得的策略信息更新参数。

对于所有强化学习的任务来说，其实目标都是使所有带衰减 reward 的累加期望最大。即如下式所示

$J(\theta) = E{(r_1 + \gamma*r_2 + \gamma^2 * r_3 +...|\pi_\theta)}$

4.3.1 策略梯度的目标函数

策略梯度的目标函数主要有以下三种方式

（1）最简单的目标函数就是初始状态收获的期望，即目标函数为：

$J_1(\theta) = V_{\pi\theta}(s1) = E_{\pi\theta}[v1]$

（2）有的问题没有明确的初始状态，那么我们的目标函数可以定义为平均价值，即

$J_{av}V(\theta) = \sum_s d^{\pi\theta}(s)V^{\pi\theta}(s)$

其中，$d^{\pi\theta}(s)$是基于策略πθ生成的马尔科夫链关于状态的静态分布

（3）使用每次time-step的平均奖励：

$J_{av}R(\theta) = \sum{_s}d^{\pi\theta}(s)\sum{_a}\pi_{\theta}(s,a)R^a_s$

为了改进策略，我们希望能够按照J(θ)的正梯度方向对π函数进行更新。假设θ是策略函数π的参数，本文的第一个基本结论为，无论上面哪种形式的J(θ)，其梯度都可以被表示为（后面会稍微证明一下）:

$\nabla_\theta J(\theta) = E_{\pi\theta}[\nabla_\theta log\pi_\theta (s,a)Q_\pi(s,a)]$

其中的

$\nabla_\theta log\pi_\theta (s,a)$

我们一般称为分值函数（score function）

我们暂定使用初始值法做目标函数

$J(\theta) = V^{\pi\theta}(s1) = E_{\pi\theta}[v1] = E(r_1 + \gamma * r_2 + \gamma^2 *r_3 + ......|\pi_\theta )$

对该目标函数进行最大化也就是在搜索一组参数向量θ，使得目标函数最大。这实际做的事改变策略概率而非改变行动轨迹的工作，所以我们接下来就要使用梯度下降求解

$\nabla_\theta J(\theta)$

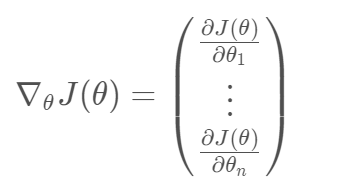
在连续策略上选用Gaussian Policy，在离散策略下采用softmax Policy

4.3.2 策略梯度定理（The policy gradient theorem）

由于我们是基于model-free的所以无法事先知道动态环境的状态分布，而奖励函数又依赖于动作和状态分布，所以无法进行求导，所以我们需要把奖励采用无偏估计的方法计算出来，首先随机采样然后取均值来估计

假设一个只有一步的MDP，对它使用策略梯度下降。πθ(s,a)表示关于参数θ的函数，映射是P(a|s,θ)。它在状态s所执行-a动作的奖励为r = R(s,a)。那么选择动作a的奖励为πθ(s,a) * R(s,a)：表示在该策略下所获得的奖励，在状态s的加权奖励为

$J(\theta) = \sum_{a \epsilon A}\pi_\theta(s,a)R(s,a)$

推导过程如下：

由于

$J(\theta) = E_{\pi\theta}[R(s,a)]$

因此

$J(\theta) = \sum_{s\epsilon S}d(s) \sum_{a \epsilon A } \pi_\theta(s,a) R(s,a)$

梯度为：

$\nabla_\theta J(\theta) = \nabla_\theta \sum_{s\epsilon S}d(s) \sum_{a \epsilon A } \pi_\theta(s,a) R(s,a)$ $\nabla_\theta J(\theta) =\sum_{s\epsilon S}d(s)\sum_{a \epsilon A } \nabla_\theta \pi_\theta(s,a) R(s,a)$

假设策略πθ为零的时候可微，则

$\because (log_a y)' = \frac{y' }{y * ln a}$ $\therefore \nabla_\theta \pi_\theta(s,a) = \pi_\theta(s,a) * \frac{\nabla_\theta \pi_\theta(s,a)} {\pi_\theta(s,a)} = \pi_\theta(s,a) * \nabla_\theta log \pi_\theta(s,a)$ $\therefore \nabla_\theta J(\theta) = \sum_{s\epsilon S}d(s) \sum_{a \epsilon A } \pi_\theta(s,a) \nabla_\theta log \pi_\theta(s,a) R(s,a)$

其中，d(s)是策略中的状态分布，π(s,a)是当前状态的动作概率分布，所以可以将策略梯度恢复成期望形式

$\nabla_\theta J(\theta) = E[\nabla_\theta log \pi_\theta(s,a) R(s,a)]$

且

$\nabla_\theta log \pi_\theta(s,a)$

为分值函数（score function）

然后在将似然率方式的策略梯度方法应用到多步MDPs上，此时因为奖励值应该为过程中的多步奖励值之和，在这里使用Qπ(s,a)代替单步奖励值R(s,a)，对于任意可微的策略梯度如下（策略价值计算公式）：

$\nabla_\theta J(\theta) = E_{\pi\theta}[\nabla_\theta log \pi_\theta(s,a) Q^{\pi\theta}(s,a)]$

策略梯度定理详细推导过程如下

策略梯度公式已经求出，并且我们的分值函数也能求出，但是关于策略函数πθ(s,a)又是如何确定的呢？

4.3.3 策略函数的设计

常用的策略函数有两种，分别是softmax策略函数和高斯策略函数

现在回头看前面策略函数πθ(s,a)的设计，在之前它一直都是一个数学符号

softmax策略函数：主要应用于离散空间，softmax策略函数使用描述状态和行为的特征
$\phi (s,a)$
与参数θ的线性组合来权衡一个行为发生的几率，即：
$\pi_\theta(s,a) = \frac{e^{\phi(s,a)^T \theta}}{ \sum_{b} e^{\phi(s,b)^T \theta}}$
其中，
$\phi_{sa}$
表示状态-动作对的L维特征向量

所以，其分值函数为：
$\nabla_\theta log\pi_\theta(s,a) = \phi(s,a) - E_{\pi\theta}[\phi(s,\cdot)]$
高斯策略函数：应用于连续行为空间的一种常用策略，通常对于均值有一个参数化的表示，同样也可以是一些特征的线性代数和：
$\mu(s) = \phi(s)^T \theta$
方差可以是固定值，也可以用参数化表示

行为对应于一个具体的数值，该数值以从
$\mu(s)$
为均值，
$\sigma$
为标准差的高斯分布中随机采样产生：
$a \sim N(\mu(s),\sigma^2)$
对应的分值函数是：
$\nabla_\theta log \pi_\theta(s,a) = \frac{(a-\mu(s)) \phi(s)}{\sigma^2}$
有了策略梯度和策略函数，我们就可以得到第一版的策略梯度算法了

4.4 蒙特卡洛策略梯度reinforce算法(不带基数)

针对具有完整Episode的情况，我们应用策略梯度理论，使用随机梯度上升来更新参数，对于公式里的期望，我们通过采样的形式来替代，即时候用t时刻的奖励（return）作为当前策略下行为价值的无偏估计，表现为：返回v(t)作为Qπ（st，at）的无偏估计，使用价值函数V(s)近似代替了Qπ（s,a）

策略梯度就可以为：

$\Delta \theta_t = \alpha \nabla_\theta log \pi_\theta (s_t,a_t) v_t$

参数更新：

$\theta_{t+1} = \theta +\alpha \nabla_\theta log \pi_\theta (s_t,a_t) v_t$

算法描述：先随机初始化策略函数的参数θ，对当前策略下的一个Episode：

${(s_1,a_1,r_2,...,s_{T-1},a_{T-1},r_T) \sim \pi_\theta}$

从t=1 到t = T-1的每一个时刻，计算个体获得的奖励v(t) ,然后更新参数θ。如此重复每一个Episode，直到结束.

算法伪代码如下：

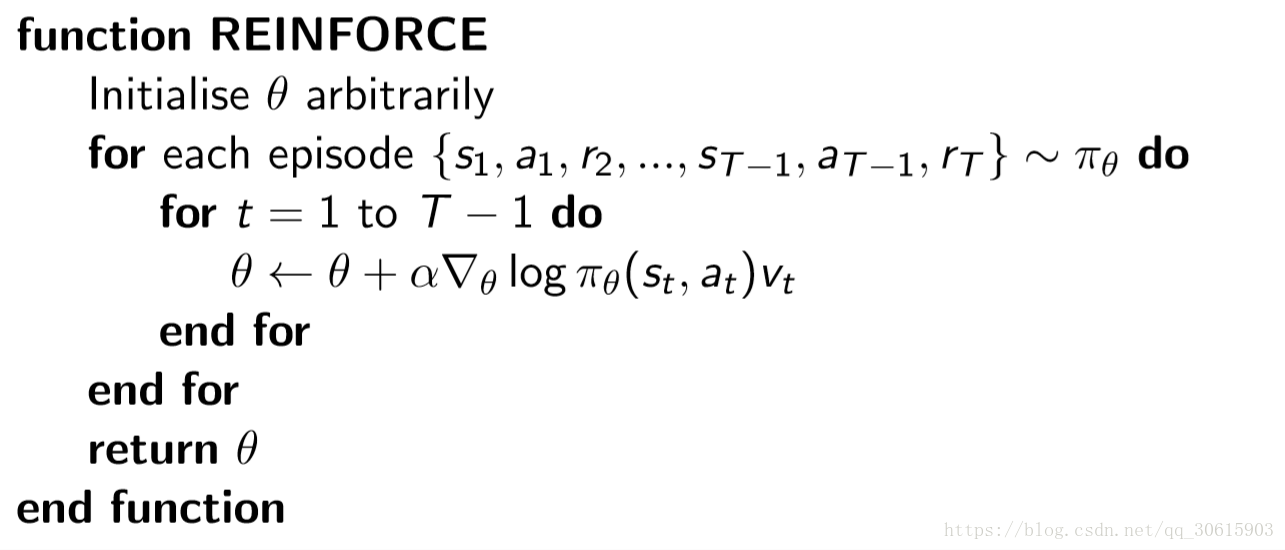
需要注意的是：

只有当一个Episode结束之后，我们才能得到该轨迹上各个状态对应的v(t)。因此该方法需要先采样一个完整的轨迹，然后在倒回来对每个状态更新参数
上面描述的Vt就是奖励，使用v而不是G可能考虑的是用它作为价值的期望，从这里也能看出这是有噪声的采样

但是该方法虽然是无偏的，但是方差非常大，所以运行速度也很慢。这个时候可以提出一个baseline来减少方差，那么如何选择baseline？

4.5 蒙特卡洛策略梯度reinforce算法（带基数）

在某些情况下，可能会出现每一个动作的奖励值都是正数，但是由于我们是通过采样的方式进行更新的，所以这时候可以引入一个基数b，则原式需要修改为

$\nabla_\theta J(\theta) = E_{\pi\theta}[\nabla_\theta log \pi_\theta (s,a)[Q^{\pi\theta} (s,a) - b(s)]]$

总结

PG算法主要是直接对策略进行更新，看过原文，对原文中有很多都没有较好的理解，因此就在网上浏览了很多的博客加强自己的理解，现在仍然比较懵，可能也是刚开始的原因，后面就要开始真真学习DRL的Policy Based方法了

前言