树
1、为什么需要树?
结合了两种数据结构的有点:(1)有序数组(2)链表
有序数组查找速度快,链表插入和删除速度快
2、有序数组中插入数据项为什么慢?
首先,要查找到新数据项待插入的位置
其次,比新数据项大的数据项全部后移,需要进行多次移动,导致很费时
2.1、有序数组的插入
插入:平均要移动数组中一半的数据项(N/2次移动),删除数据项也需要多次移动,非常耗时
3、链表中查找太慢?
链表的插入和删除都很快,因为只需要改变引用值就可以了,时间复杂度为O(1)
但查找,必须从头开始,依次访问链表中的每一个数据项,直到找到该数据为止。
查找:平均要访问N/2个数据项,把每个数据项的值和要查找的数据项作比较,这个很慢。
数据存储结构
常见的数据存储方式有两种:(1)顺序存储(数组)(2)非顺序存储(链表)
1、有序数组
当我们平常在一组相关类型的变量集合中进行查询搜索时,通常使用有序数组的存储方式,因为时间复杂度从O(n)降低为O(log n),因此查询速度快
但是在进行相关的增删时,为了保证有序性,可能要进行大量的移动,因此比较耗时
2、链表
但我们的内存空间并不一定都是连续的,因此就有了另一种存储方式:链表存储
利用链表存储,就能有效的将这些零散的碎片空间存储下来,因为链表中有一块区域是存储的指向下一个数据的指针,因此链表在插入和删除时,比较容易,只需要改变指针指向的位置即可。
但是在进行查询时,必须要从头一个个向后找,比较耗时。
3、二叉查找树(BST)
针对有序数组和链表的优点,又引出了一种树形存储结构(二叉查找树),结合了有序数组和链表的优点:
使得,在树中查找数据时,其速度和在有序数组中查找一样快;
在插入数据和删除数据时,和在链表中一样快
可点击二叉查找树在线演示,进行实战演示,在比较理想的情况下,二叉查找树可能如下图所示
从下图中也可以看出,二叉查找树的特点:左子树的节点值比父节点小,右子树的节点值比父节点大。
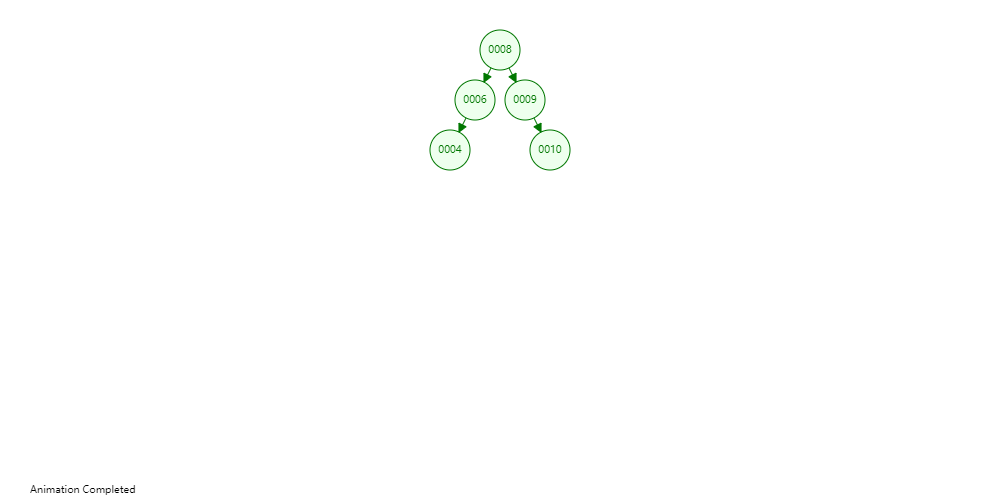
4、平衡二叉树
由于二叉查找树的特点,当我们输入的是一组有序序列时,二叉查找树又会退化成链表结构,其时间复杂度又变成O(n)。
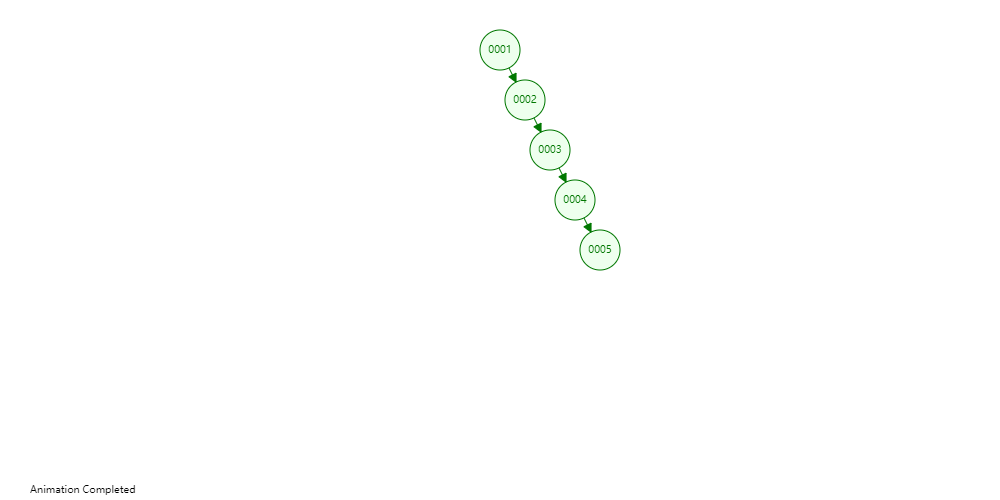
为了解决这个问题,就引入了平衡二叉树的概念。
平衡二叉树(balanced binary tree)的定义:
- 又称为AVL树(Adelson-Velskii and Labdis)
- 一颗平衡二叉树或者是空树,或者是具有下列性质的二叉排序树:
(1)左子树与右子树的高度之差的绝对值小于等于1
(2)左子树和右子树也是平衡二叉排序树
这样,在二叉查找树的插入过程中,通过左旋和右旋等操作就能解决二叉查找树的缺点。使得对于有n个节点的平衡树,其最坏的时间查找复杂度也为O(log n)
可点击平衡二叉树在线练习,进行实战演示
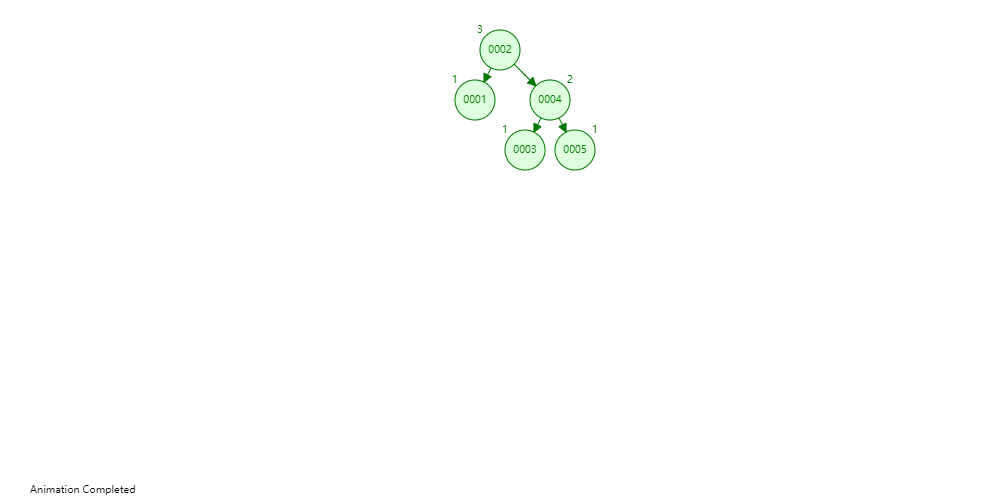
4.1 如何判断二叉树是否为平衡二叉树?
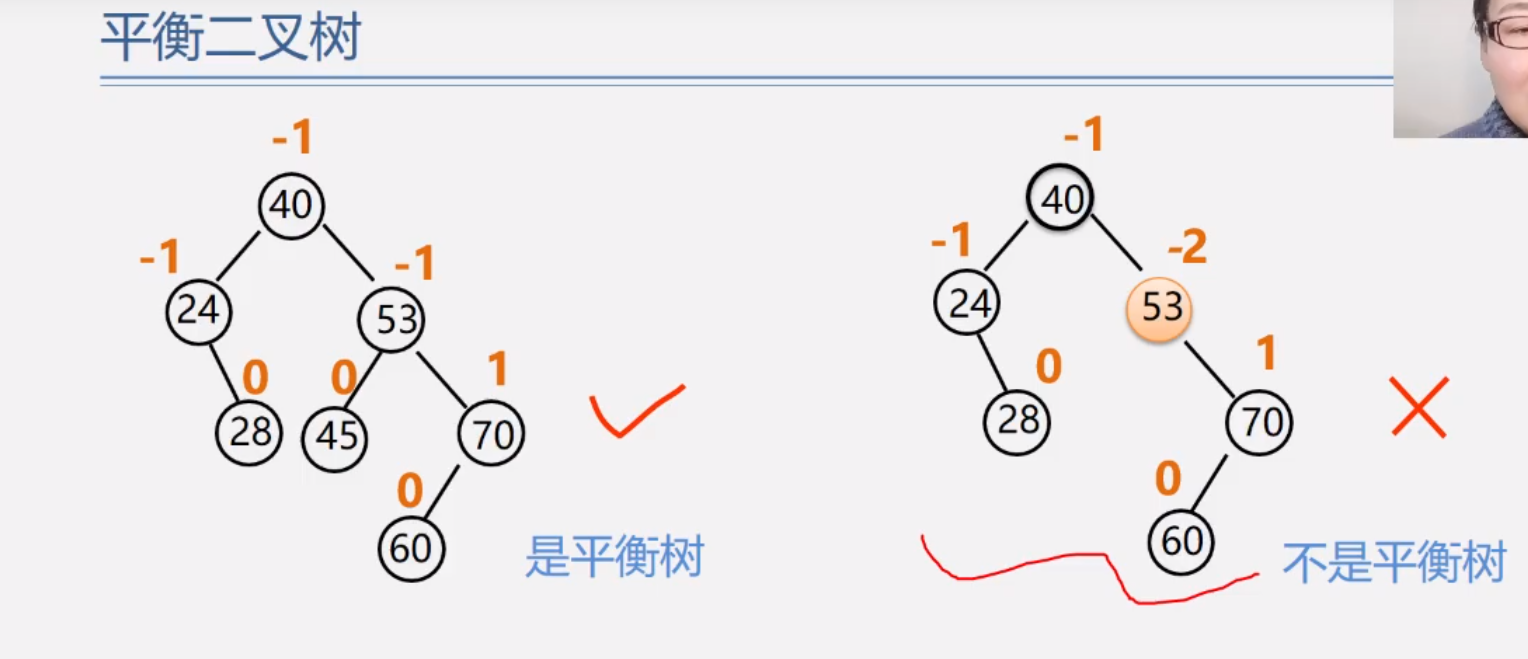
为了方便起见,给每个结点附加一个数字,给出该结点左子树与右子树的高度差,这个数字称为结点的平衡因子(BF)。
平衡因子 = 结点左子树的高度 - 结点右子树的高度
根据平衡二叉树的定义,平衡二叉树上所有结点的平衡因子只能是-1、0或者1
4.2 失衡二叉树
在二叉查找树的插入和删除过程中,往往会导致二叉树的失衡,且可能存在多个失衡结点,此时:
当不止一个失衡结点时,失衡结点取最小失衡子树的根结点,如下图中的7和16都为失衡结点,但16的子树结点个数更少,因此选择16作为失衡结点。
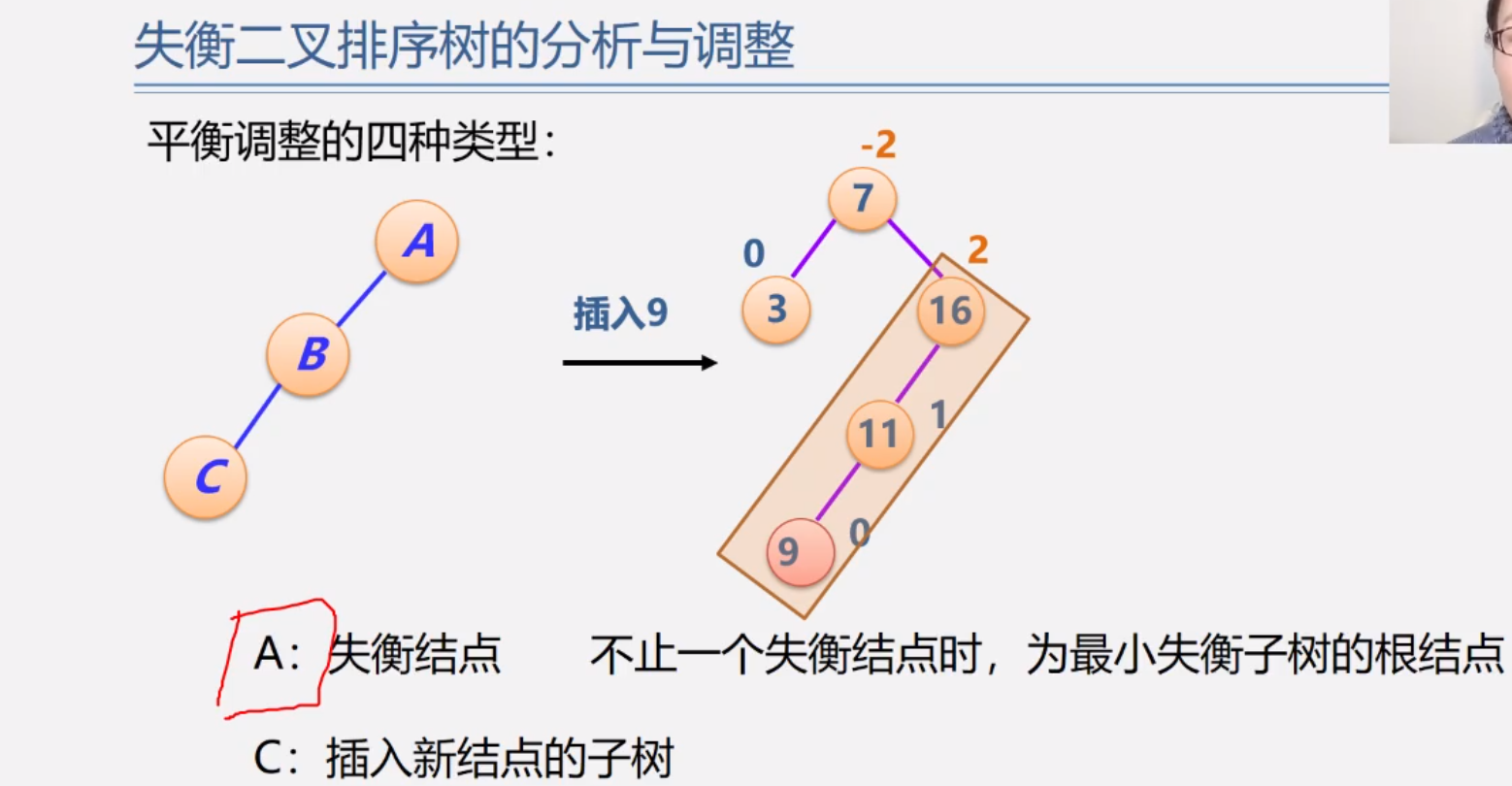
失衡时,往往会出现如下四种情况,这四种情况也可以称为失衡二叉树
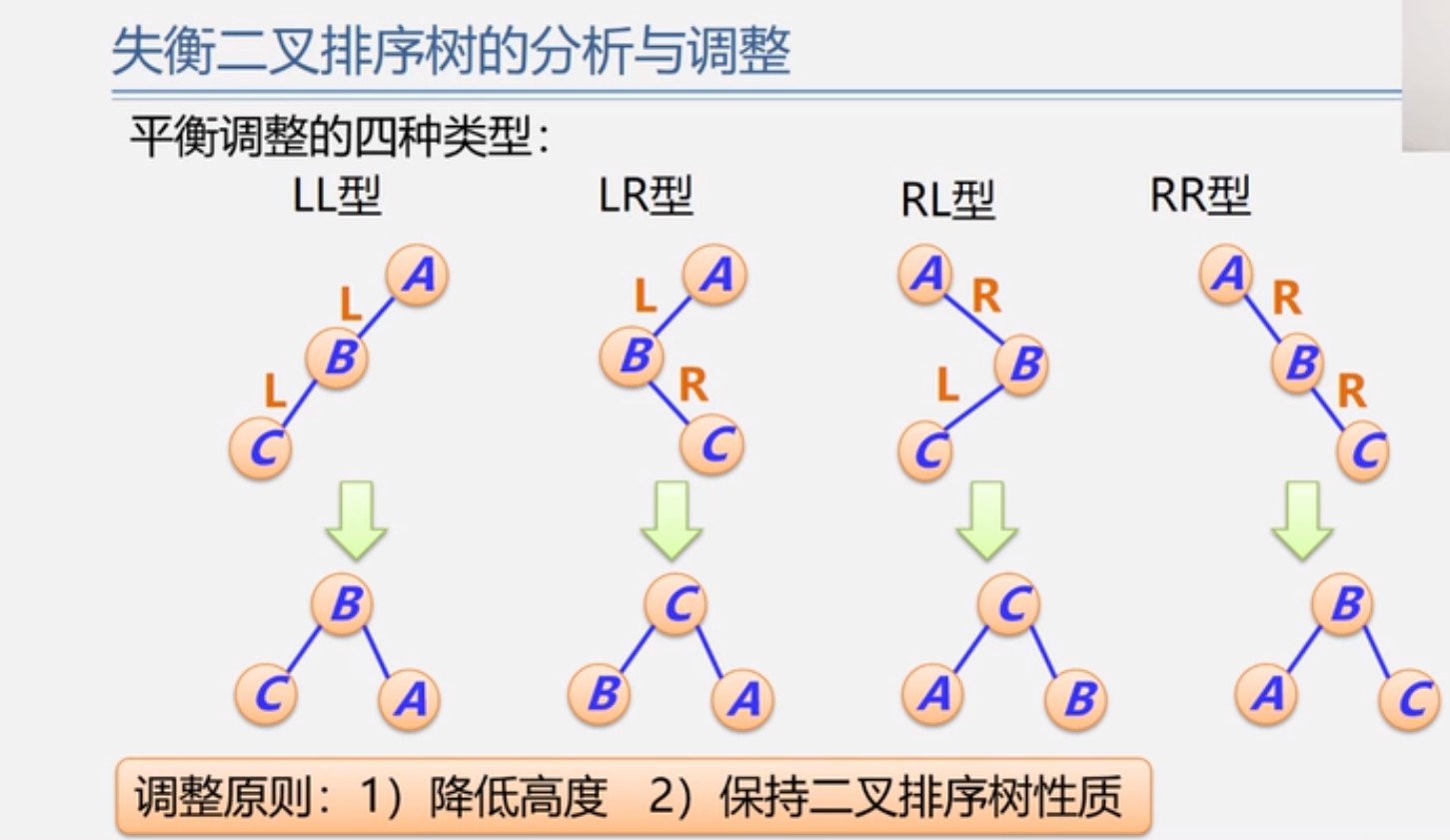
4.2.1 LL型的调整过程
以下图为例,C表示要插入的新结点,当插入C之后,可能会导致A失衡,此时A称为失衡结点。
根据二叉排序树的特性,左子树小于根节点小于右子树,可以得出如下信息:
调整前:C < B < A,但A为根结点(失衡结点)
调整后:C < B < A,B为根结点,才能保证该树平衡
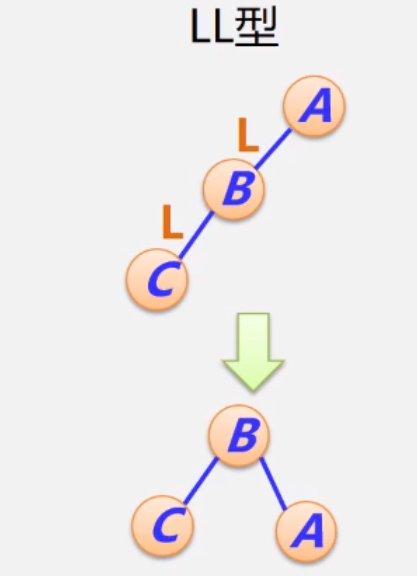
调整过程:
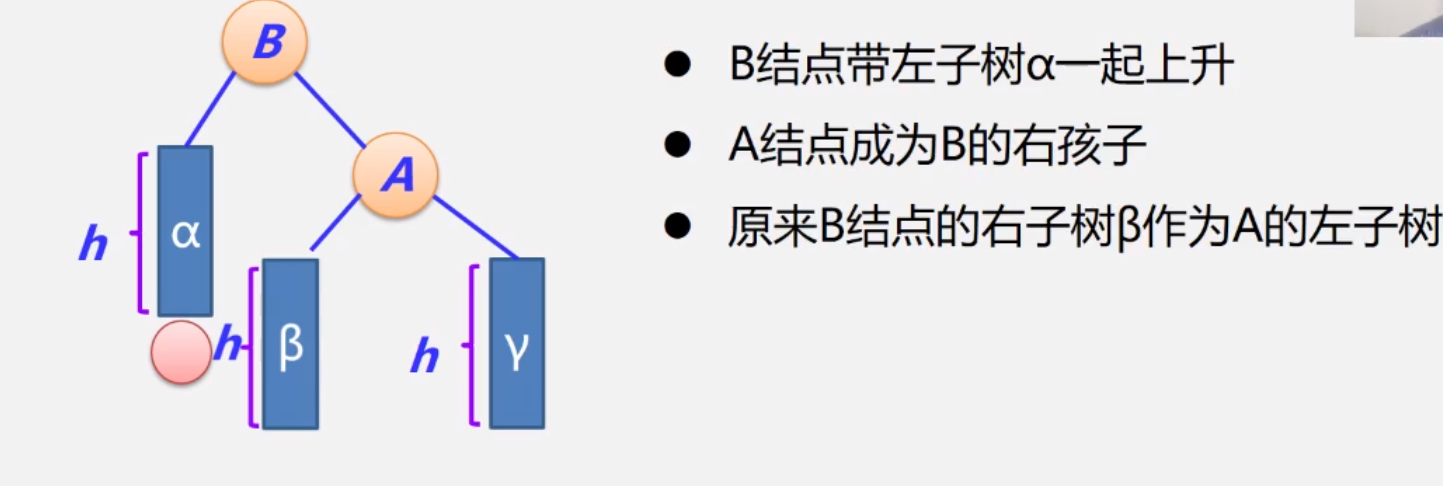
调整前,下图所示,在α后面新增一个结点,满足LL型的插入
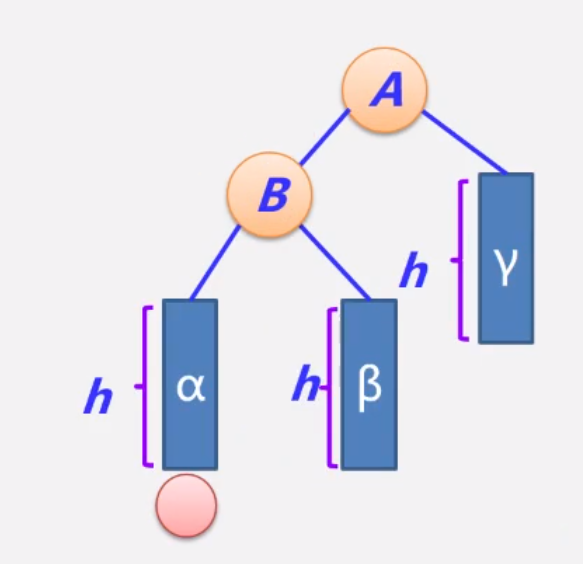
调整后,如图所示,手写一遍,就明白了,一定要手写,加强理解
4.2.2 RR型的调整过程
调整前:A < B < C,但A为根结点(失衡结点)
调整后:A < B < C,B为根结点,才能保证该树平衡
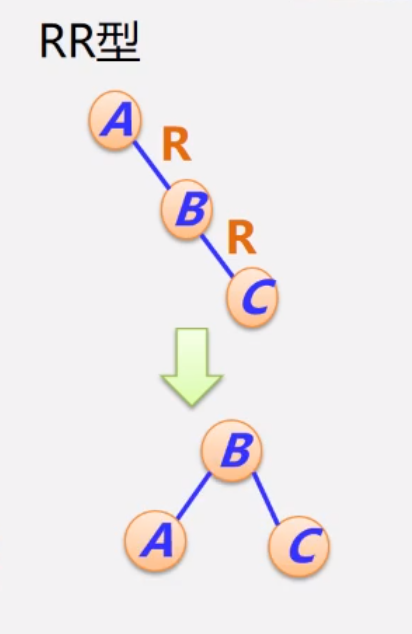
调整前:在β后面新加入一个结点,满足RR型
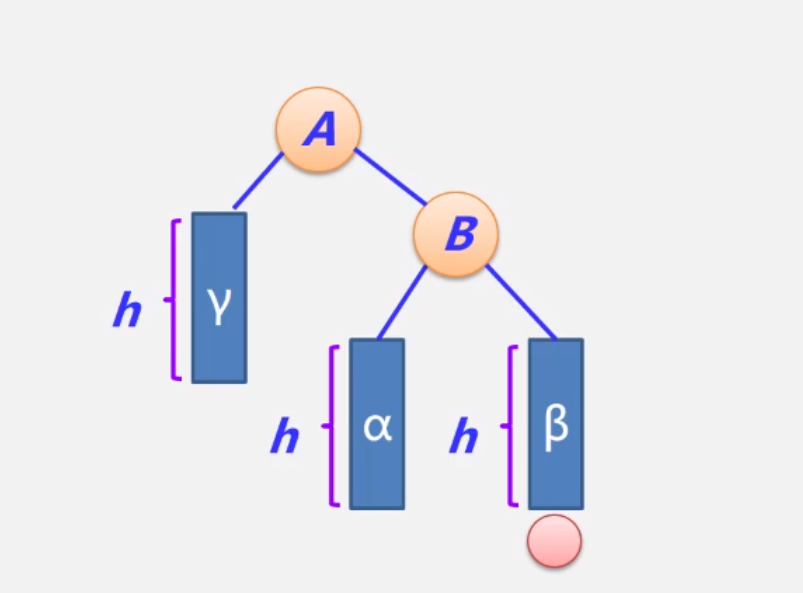
调整后:
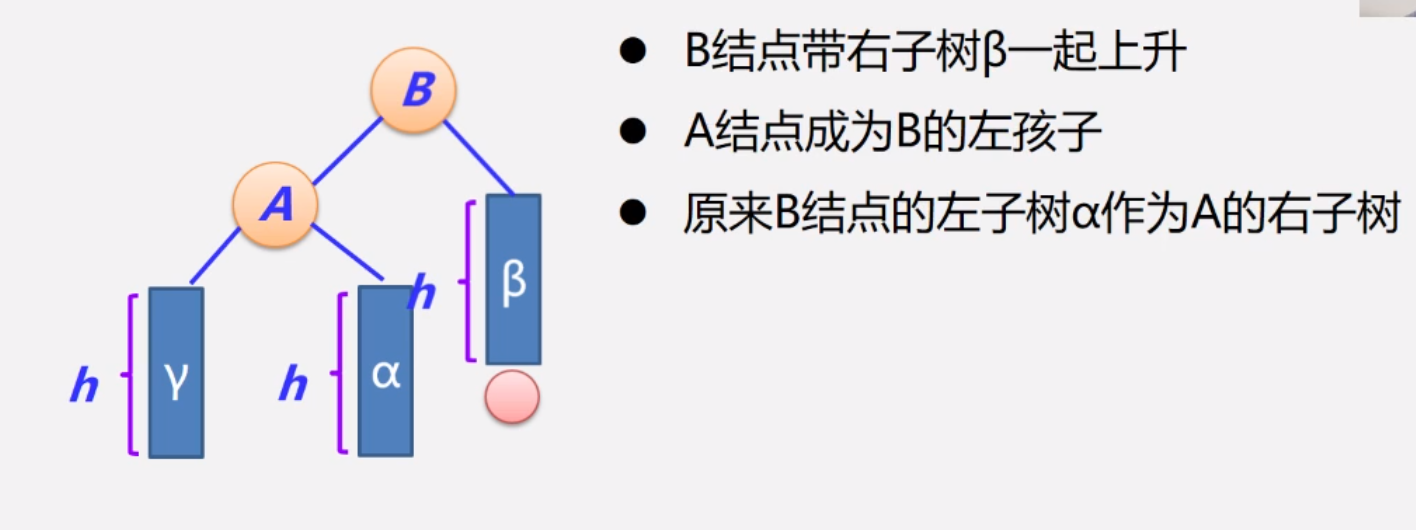
4.2.3 LR型的调整过程
调整前:B < C < A,但A为根结点(失衡结点)
调整后:B < C < A,C为根结点,才能保证该树平衡
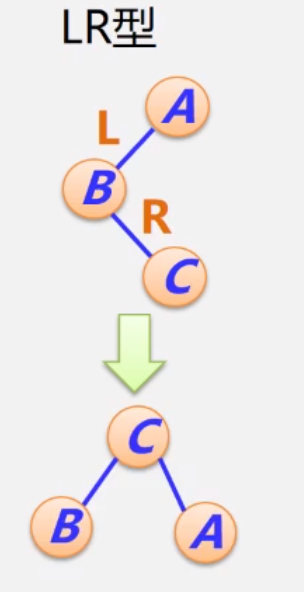
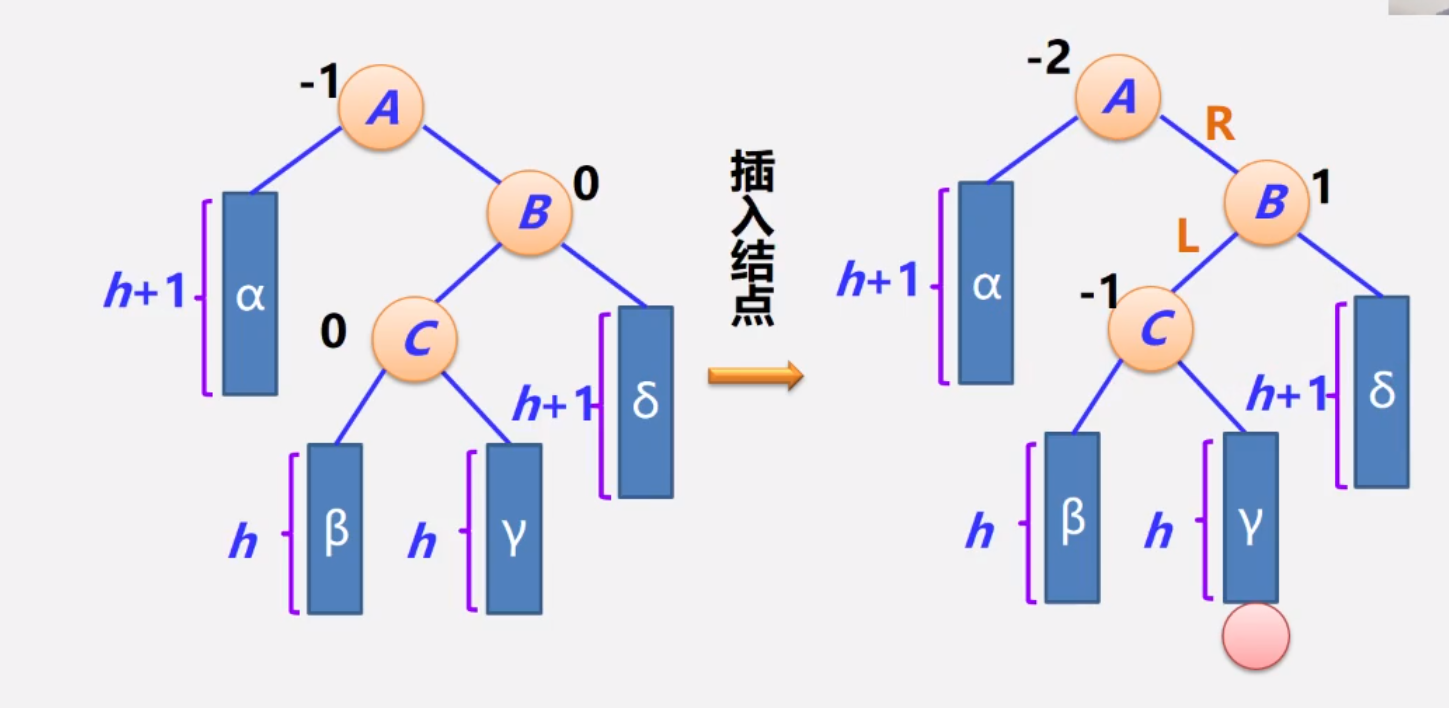
调整前:在β后面新增一个结点,导致A失衡。
假设γ和β的高度都为h,则α和C同高度,就都为h+1,因此δ的高度为h+1(因为A的平衡因子为1,左子树要比右子树的高度大1,而B的高度为h+2,所以δ的高度为h+1)
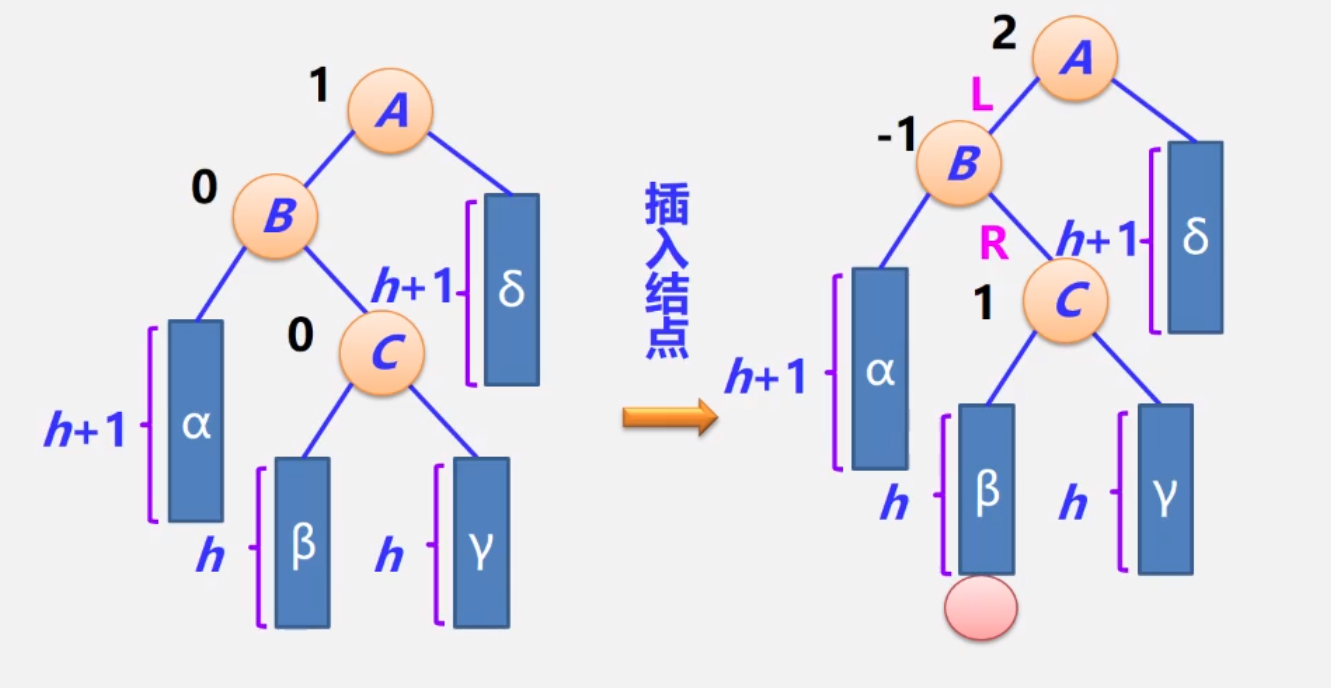
调整后:
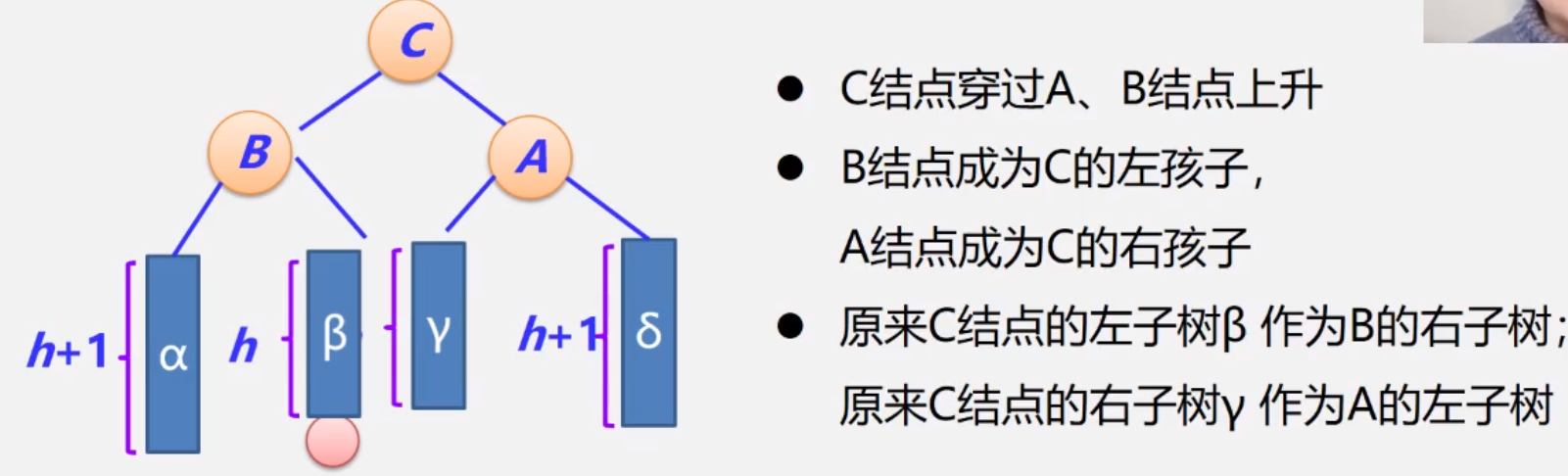
4.2.4 RL型的调整过程
调整前:C < B < A,但A为根结点(失衡结点)
调整后:C < B < A,B为根结点,才能保证该树平衡
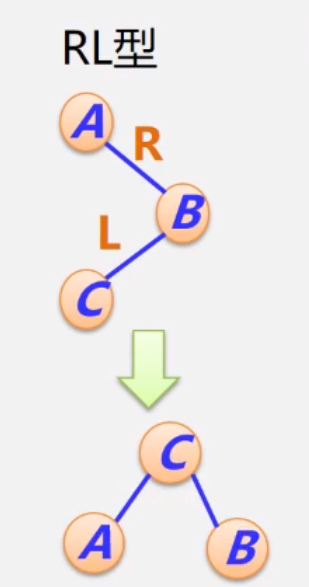
调整前:
调整后,可参考4.2.3小节来模拟(明白LR就可以明白RL了)
4.3 平衡二叉树的删除
后续在学习
5、2-3树
因为平衡二叉树要求每个节点的左子树和右子树的高度差不超过1,这个要求实在太严格,导致每次进行插入/删除节点的时候,几乎都会破坏平衡二叉树的第二个规则,因此总是需要左旋和右旋来调整,使之再次成为一颗符合要求的平衡树。
如果在那种插入、删除很频繁的场景中,平衡树需要频繁的进行调整,会使得平衡树的性能大打折扣;
那么有没有绝对平衡的一种树呢?没有高度差也不会有平衡因子,没有平衡因子也就不会调整旋转等操作。
为了解决这个问题,就有了2-3树。2-3树正是一种绝对平衡的树,任意结点到它所有叶子节点的深度都是相等的。
5.2.1 2-3树的性质
2-3树是一种多路查找树,2和3的意思就是2-3树包含两种特点:
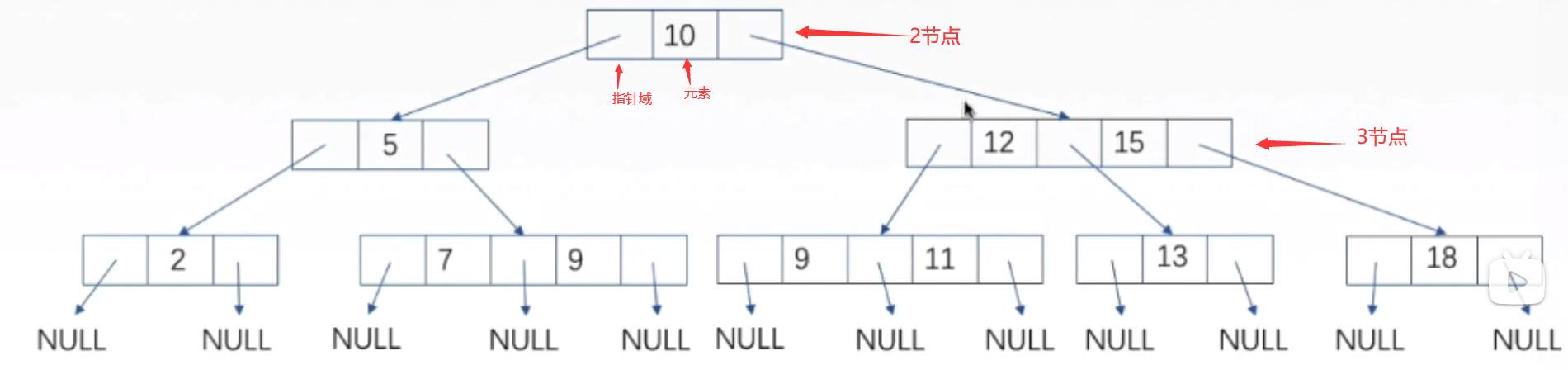
(1)2节点:包含一个元素(数据域)和两条链接(指针域)
2节点要么有两个孩子,要么没有孩子,不允许只有一个孩子
(2)3节点:包含一大一小两个元素(数据域)和三个链接(指针域)(两个元素按大小顺序排序好)
3节点要么有三个孩子,要么就没有孩子,不允许有一个或两个孩子
(3)2-3树所有叶子节点都在同一层次
(4)插入结点时不能将该节点插入到一个空节点上,新的结点只能通过分裂或者融合产生
(5)当2-3树只有2节点的时候,其只能是一颗满二叉树(完美二叉树)
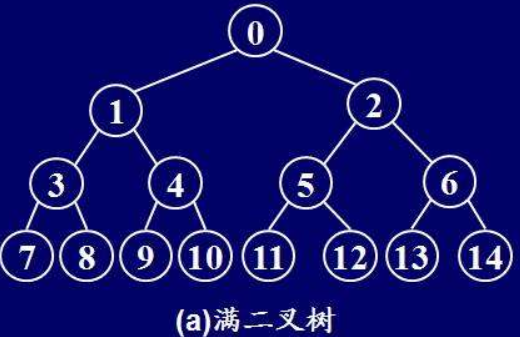
5.2.2 满二叉树介绍
一个二叉树,如果每一个层的节点数都达到最大值,则这个二叉树就是满二叉树
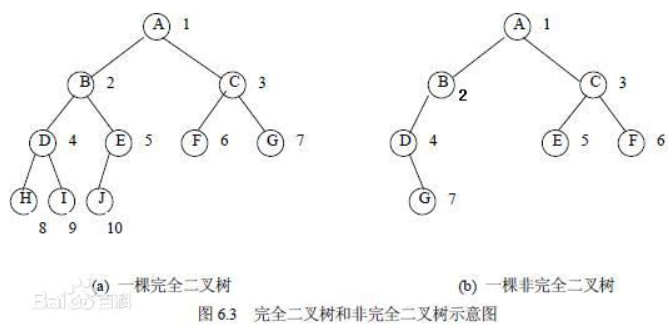
5.2.3 完全二叉树介绍
假设二叉树的深度为h,除第h层外,其他各层(1~h-1)的结点数都达到最大个数,第h层所有的节点都连续集中在最左边,这就是完全二叉树。
5.2.4 2-3树的插入
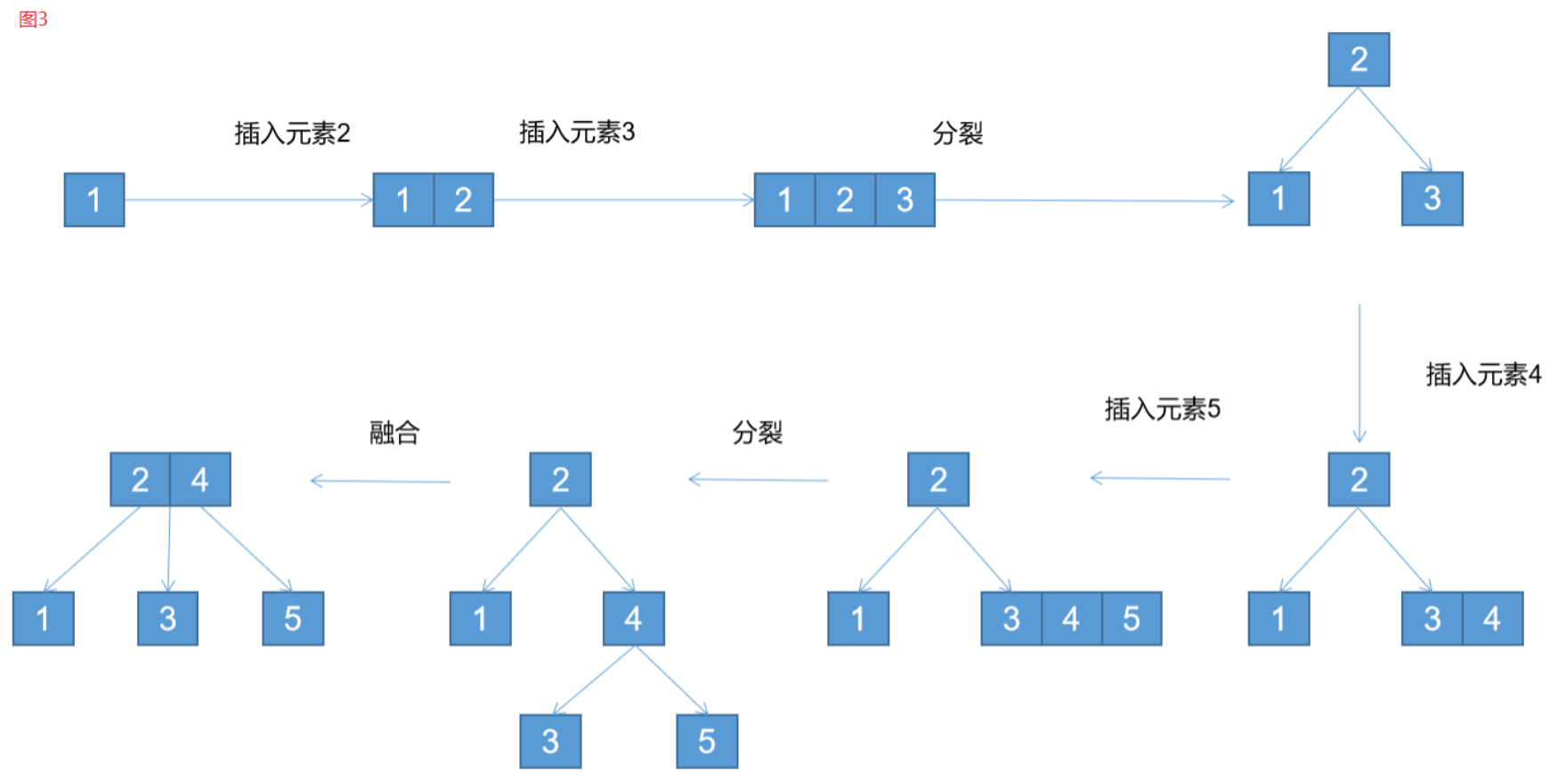
插入过程:
如上图所示,依次插入(1,2,3,4,5)五个元素
(1)插入元素1:创建一个2节点(元素为1)
(2)插入元素2:其1,2元素融合暂时形成一个3节点,
为什么2元素不能生成一个节点作为1元素所在节点的右孩子?
因为插入结点时不能将该节点插入到一个空节点上,新的结点只能通过分裂或者融合产生。
(3)插入元素3:其1,2,3元素暂时融合形成一个4节点
开始分裂,因为这是一颗2-3树,不存在4节点,所以暂时形成的4节点要开始分裂,将中间的元素作为根节点,左右两个元素各位其左右孩子节点,形成一颗满二叉树
(4)插入元素4:根据元素大小,与元素3形成一个3节点(新节点不能插入到一个空节点)
(5)插入元素5:根据元素大小,插入到3,4所在的3节点上,暂时形成一个4节点
开始分裂,3,4,5开始分裂为:4为根节点,3,5各自作为4的左右孩子
开始融合,根据2-3树的特点:所有叶子节点都在同一层或2-3树只有2节点时,只能是一颗满二叉树的性质,所以2-3树要向上融合满足2-3树的性质,因此将4元素向上融合,与元素2组成一个3节点
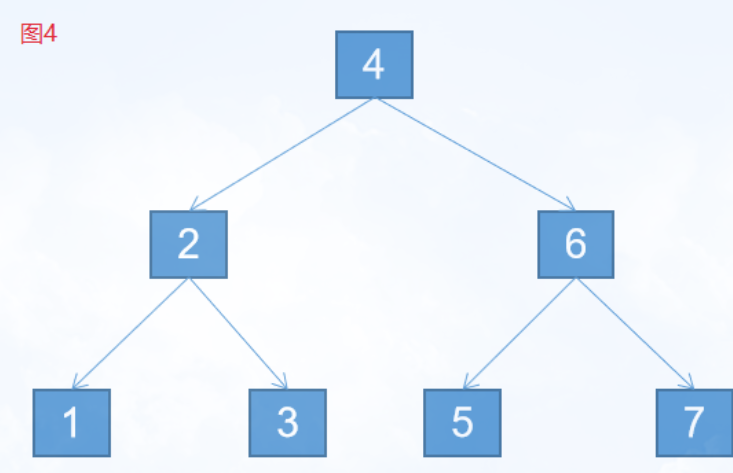
继续插入6,7元素,根据分裂和融合,可以形成最终的上图所在的满二叉树
6、红黑树
由于将2-3树这种直白的表述写成代码实现起来并不方便,因为需要处理的情况太多,需要维护两种不同类型的节点,将链接和其他信息从一个节点复制到另一个结点,将结点从一种类型转换为另一种类型等等。
因此,红黑树出现了,红黑树背后的逻辑就是2-3树的逻辑。
6.1 红黑树的定义
(1)红黑树具备二分搜索树的所有性质
(2)红黑树的根节点是黑色的
(3)红黑树的每个节点是红色的,或者是黑色的
红色表示2-3树中的3节点中的左值
(4)如果一个节点是红色的,那么它的孩子都是黑色的
(5)每个叶子节点(红黑树中叶子节点为最后的空节点)是黑色的
(6)从任意一个节点到叶子节点经过的黑色节点时一样的
红黑树的示意图如下,其叶子节点为NIL的节点,并非其中的10、50、140等等
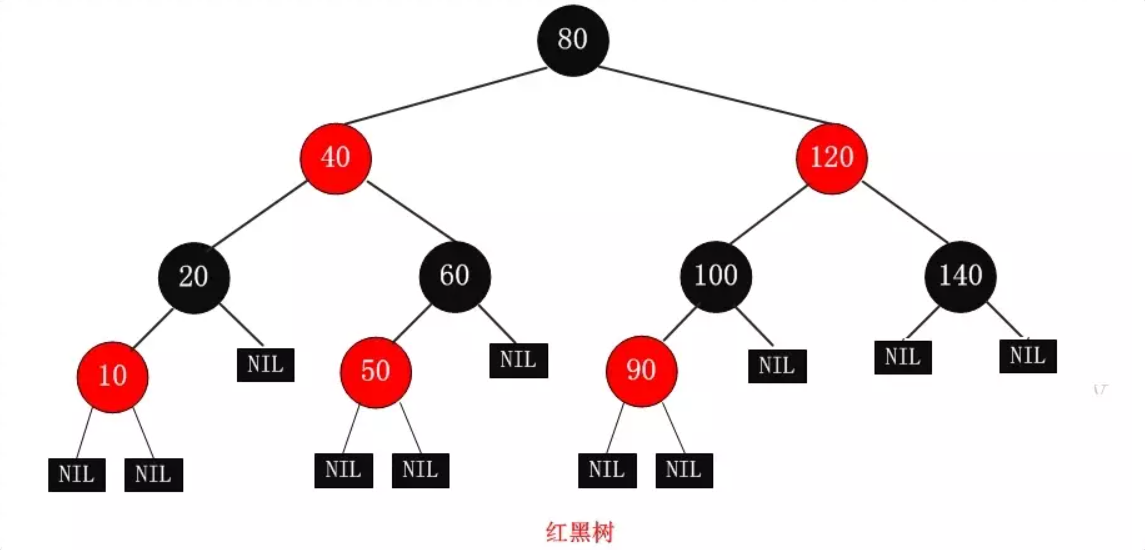
6.2 左倾红黑树与2-3树的等价性
红黑树的另一种定义:
(1)红链接均为左链接
红色表示2-3树中的3节点中的左值
(2)没有任何一个节点同时和两条红链接相连
在2-3树中,不存在永久的4节点,4节点终究要分解,因此2-3树中没有任何一个节点能同时和两条红链接相连
(3)该树是完美黑色平衡的,即任意空链接到根节点的路径上的黑链接数量相同(和2-3树是等价的,任意节点到其叶子节点的高度是相同的)
2-3树是完美平衡的,将3节点转成二叉树只增加了左红链接,其他黑色链接没有什么变化,依然是黑色平衡的。
2-3树与红黑树的关系比较
(1)2-3树中的2节点[a]转换为红黑树的黑色结点[a]
(2)2-3树中的3节点[b,c]可以转换为红黑色中的[b,c],其红黑树中,c为黑色节点,b为红色节点。
因为 b < c ,所以b作为c的左孩子下移,使用红色边表示b和c存在并列关系,表示在2-3树中b与c保存在一个3节点中;
在实际代码中,没有必要定义一个边的类,由于节点b和红色边是一一对应关系,所以可以将节点b标记为红色,表示节点与其唯一的父节点是并列关系。
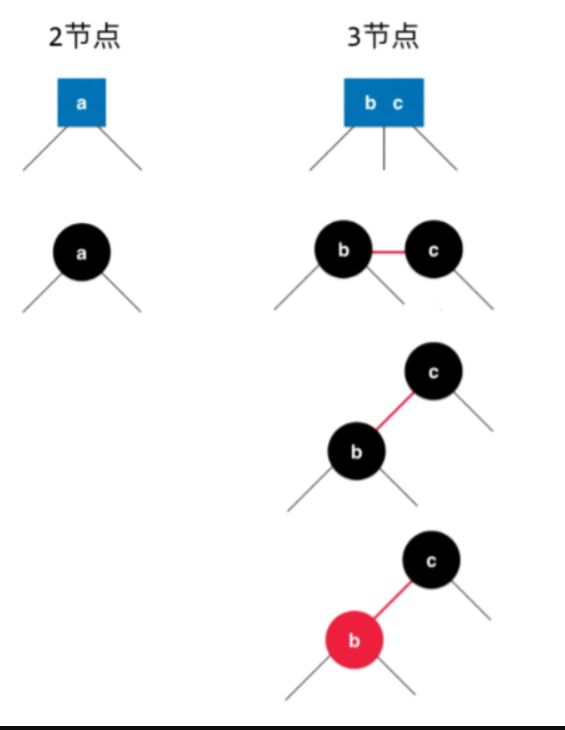
如上图所示,把这种2-3树转换后,节点分为红黑节点的树称为红黑树。根绝红黑树的转换过程,可以知道红色节点都是左倾斜的,这不是推导出来的,而是定义出来的。
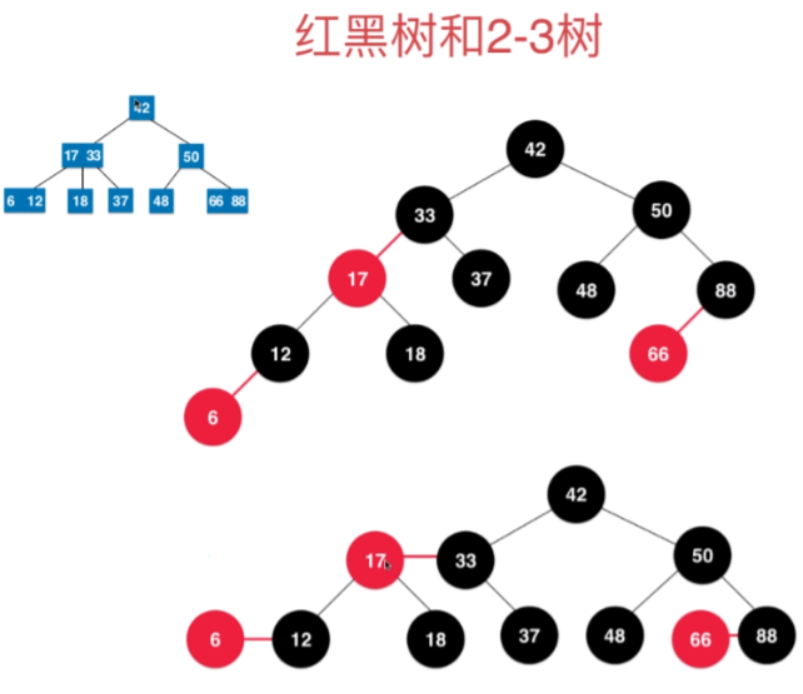
6.3 2-3树到红黑树的转换规则
2-3树有两类节点:2节点和3节点,还有一个临时的4节点
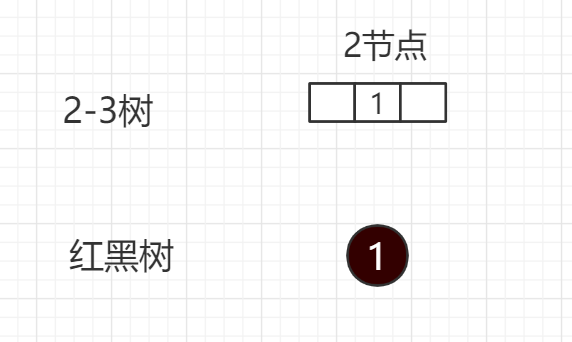
2节点:
(1)2-3树:生成一个2节点,存储元素1
(2)红黑树:对应于一个黑色节点
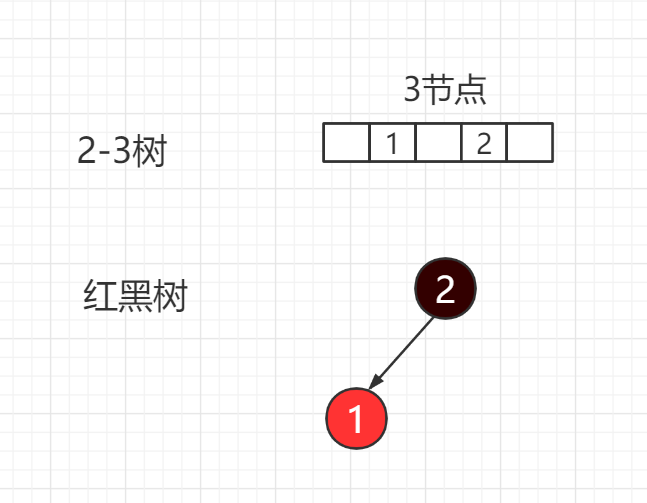
3节点:
(1)2-3树:生成一个3节点
(2)按照左倾红黑树与2-3树的等价性,且2>1,因此2为黑色根节点,1为红色子节点
对应于红黑树黑色的父节点和红色的左孩子节点
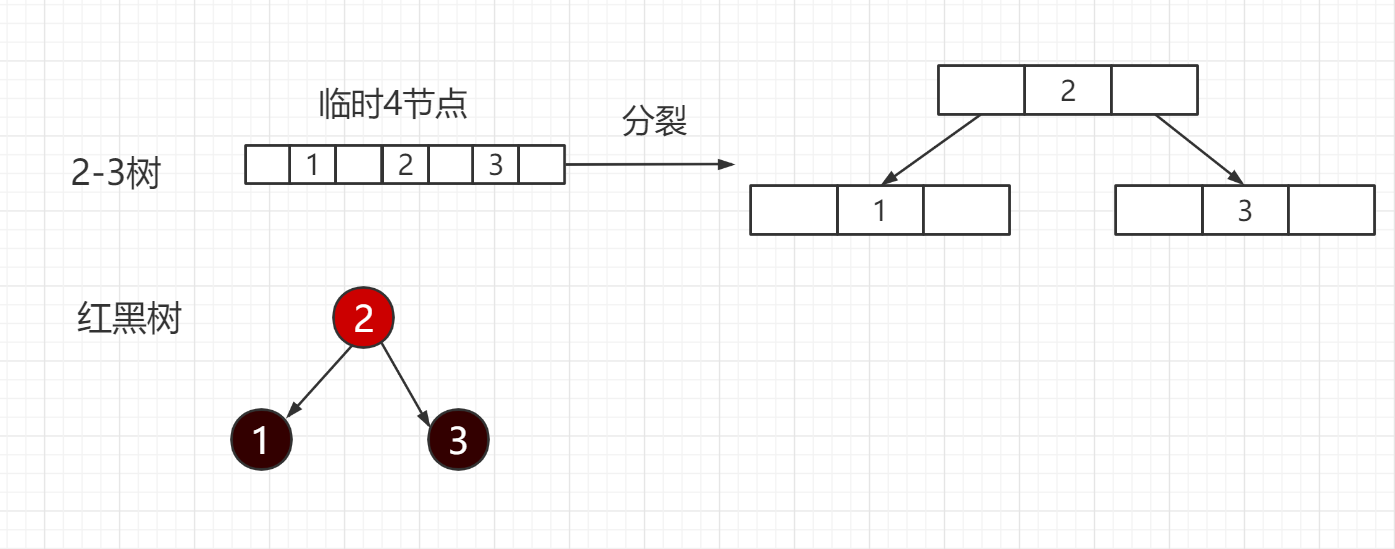
临时4节点:
(1)2-3树:生成一个临时4节点,进行分裂
(2)对应于红黑树红色父节点和黑色的左右孩子节点
为什么父节点是红色而不是黑色?是为了符合红黑树中插入任何一个节点默认都是红色的实现方式
如果该父节点是根节点,那么它肯定需要变色这一点就不属于2-3树向红黑树得的变换规则了,而属于红黑树的性质
6.4 红黑树的旋转、变色和颜色反转
分别向2-3树和红黑树中依次插入(1,2,3)三个元素来看旋转、变色和颜色反转的过程
红黑树的一个性质:根节点必须为黑色的。
一个实现红黑树的规则:新插入的节点永远为红色
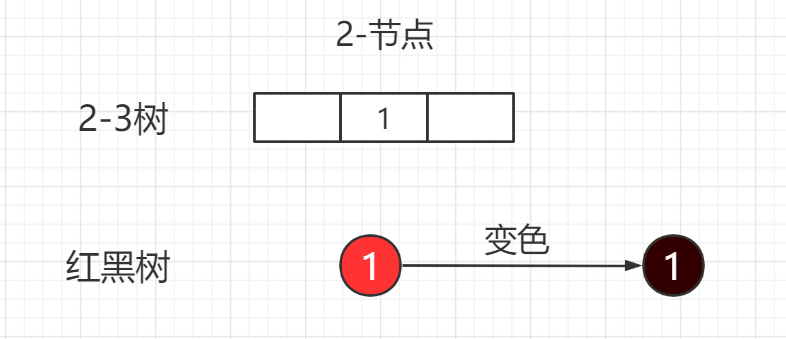
如上图所示,插入元素1
2-3树就是一个2节点,不需要做任何改变
根据红黑树添加的规则:新插入的节点为红色,所以1元素的节点为红色。根据红黑树的性质:根节点必须为黑色,所以1元素的节点需要进行变色。
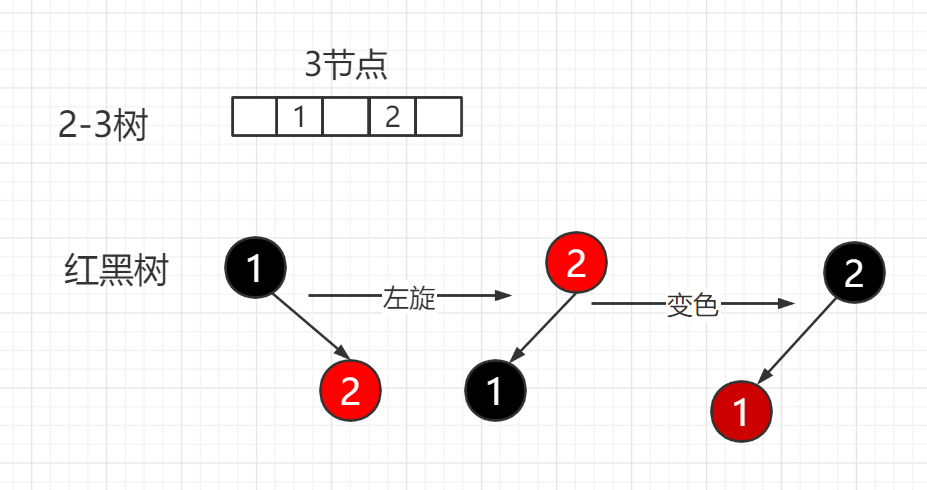
插入元素2:
(1)插入元素2,2-3树会形成一个3节点。
(2)根据2-3树向红黑树的转换规则,需要变为2元素所在的节点为黑色的父节点,1元素所在的节点为红色,并为2元素的左孩子节点。
左旋:根据二分搜索树的性质,插入的2元素会成为1元素的右孩子,这时需要我们对1元素进行左旋转,然后得到如上左旋转后的结果。
变色:再将2元素换为1元素的颜色,然后将1元素变为红色。
为什么这样变色?首先为向上兼容,该字数的根节点需要始终保持原来的颜色,即新的根节点2换成原来的根节点的颜色。其次,根据2-3树中3节点的左值均为红色,需要将1节点的颜色变为红色。
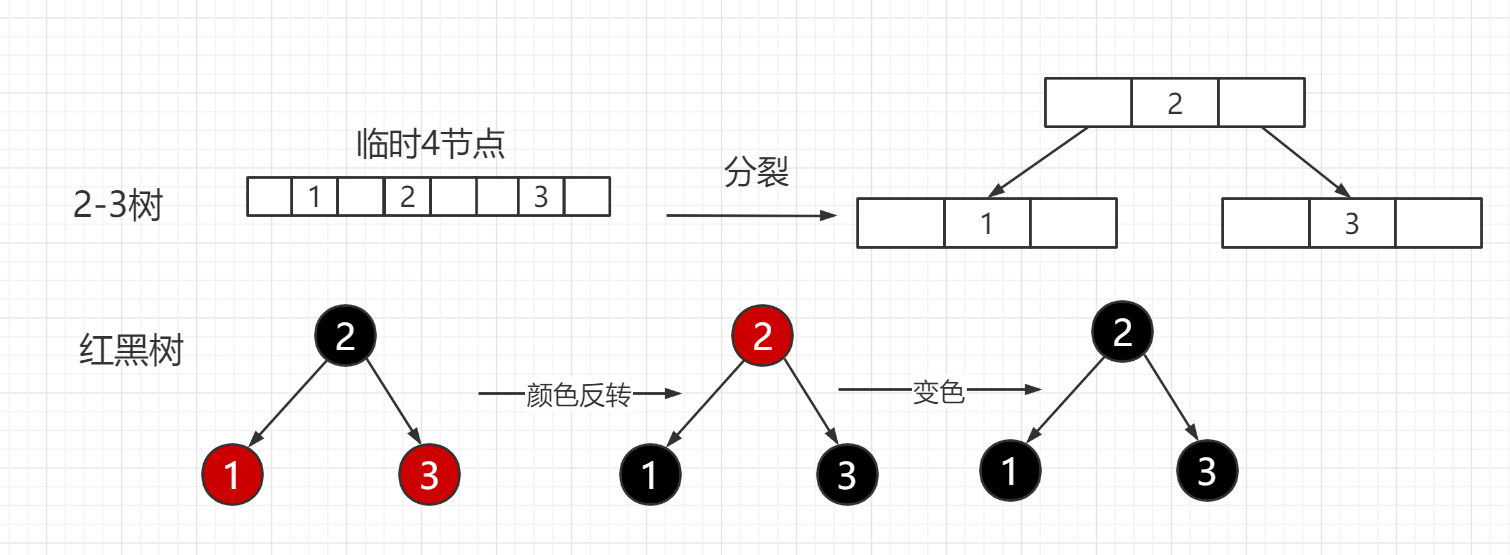
插入元素3:
(1)2-3树:生成临时4节点,进行分裂
(2)红黑树:新插入的节点都是红色的,所以,这时会形成一个根节点为2,左右孩子都是红色的节点
颜色反转:根据2-3树向红黑树变化的规则,并不满足。需要进行颜色反转,即将1,3元素变为黑色,2元素变为红色。
为什么这样进行颜色反转?因为在2-3树中,4节点分裂后要向上融合。
变色:这时2元素为根节点,根据红黑树的性质,需要进行变色即可。如果2元素不是根节点,需要向上融合,如6.3所示
6.4.1 旋转
在插入或者删除操作中可能会出现右倾或者两条连续的红链接,在向上变换的过程中(恢复)都要调整为左倾。
6.4.1.1 左旋转
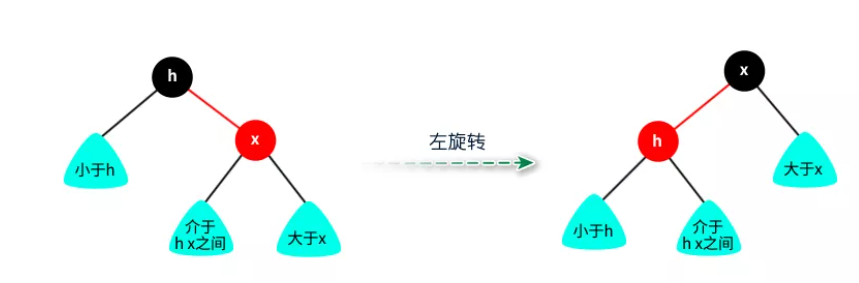
假设有一条红色的右链接需要转为左链接,如下图所示:
这个操作叫做左旋转,右链接变成左链接,意味着被红链接指向的节点会变成红色,根节点默认是黑色
6.4.1.2 右旋转
右旋转也一样,不过在左倾红黑树中,只有出现两条连续红色的左链接才会进行右旋转。

6.4.2 颜色变换
颜色变化是用在临时4-节点上的,不管是向下变换还是向上变换。

总结
通过上面依次插入(1,2,3)的过程,我们总结一个规律:
(1)右旋:当一个节点的左孩子节点和左孩子节点都是红色的时候,需要右旋
(2)左旋:当一个节点的右孩子是红色节点并且左孩子不是红色,需要左旋
(3)颜色反转:当一个节点的左右孩子节点都是红色的时候需要进行颜色反转
6.5 红黑树的删除
后续待学习